百木园-与人分享，
就是让自己快乐。
当前位置：百木园 > 野生技术 > 正文

经典动态规划题（python）

2023-03-29 分类：野生技术 阅读(207) 评论(0)

python 动态规划

性质

  1. 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
  2. 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。
  3. 无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

动态规划中的子问题往往不是相互独立的（即子问题重叠）。在求解的过程中，许多子问题的解被反复地使用。为了避免重复计算，动态规划算法采用了填表来保存子问题解的方法。

适用问题

适合用动态规划来解决的问题，都具有下面三个特点：最优化原理、无后效性、有重叠子问题。

（1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

（2）无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

（3）有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势。
算法实现
动态规划三要素：

（1）问题的阶段

（2）每个阶段的状态

（3）相邻两个阶段之间的递推关系

整个求解过程可以用一张最优决策表来描述，最优决策表是一张二维表（行：决策阶段，列：问题的状态）表格需要填写的数据一般对应此问题的在某个阶段某个状态下的最优值（如最短路径，最长公共子序列，最大价值等），填表的过程就是根据递推关系，最后根据整个表格的数据通过简单的取舍或者运算求得问题的最优解。

例如：f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}

1. 背包问题

假设我们有n种类型的物品，分别编号为1, 2...n。其中编号为i的物品价值为vi，它的重量为wi。为了简化问题，假定价值和重量都是整数值。现在，假设我们有一个背包，它能够承载的重量是Cap。现在，我们希望往包里装这些物品，使得包里装的物品价值最大化，那么我们该如何来选择装的东西呢？注意：每种物品只有一件，可以选择放或者不放。初始化数据为：n=5，w={2,2,6,5,4}，v={6,3,5,4,6}，Cap=10

情况1: 如果第i件物品不能放（即这个物品的重量直接大于了当前限重v），则问题转化为“前i-1件物品放入容量为v的背包中”，即f[i-1][v]；

情况2: 如果放第i件物品是可以放也可以不放，则问题转化为：

​ 1）、如果选择不放第i件物品，则问题转化为“前i-1件物品放入容量为v的背包中”，即变大时f[i-1][v]；

​ 2）、如果选择放第i件物品，则问题转化为“前i-1件物品放入剩下的容量为v-w[i]的背包中”，此时能获得的最大价值就是f [i-1][v-w[i]]再加上通过放入第i件物品获得的价值v[i]。

最优子结构描述如下：当子问题f[i][v]是最优时，其子问题f[i-1][v]和f[i-1][v-w[i]]（中的较大者）显然同样也必须是最优的值，不然在情况1或者情况2下总会矛盾。

B) 递归定义最优解的值

根据上面的分析，显然子问题

f[i][v]=f[i-1][v]，这时是情况1

f[i][v]=max{f[i-1][v], f[i-1][v-w[i]]+v[i] }，这时是情况2。

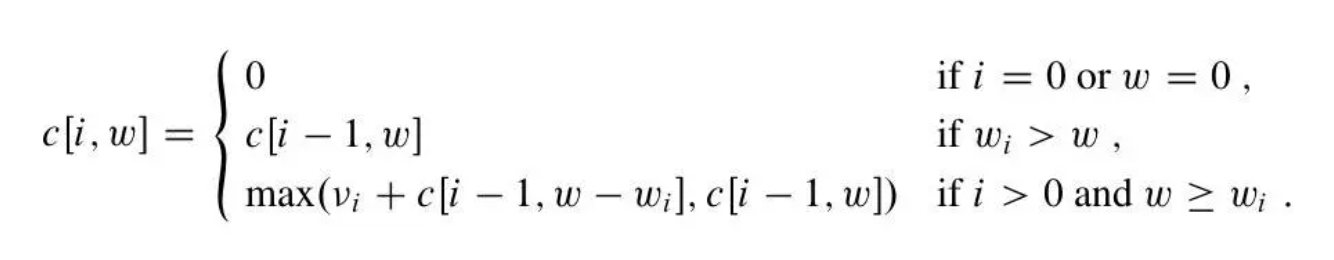
image-20230328201513285

import numpy as np

def solve(num,Weight,wlist,pricelist):
    a = np.array([[0]*(Weight+1)]*(num+1))
    #用numpy新建一个数组出来，每一个值都表示当前情况下的最油重量，
    # 坐标即为放第i个物品，以及当前容量
    for i in range(1,num+1):
        for j in range(1,Weight+1):
            if wlist[i-1] > j:
                a[i,j] = a[i-1,j]#如果当前要放的超过了当前容量，就不放了
            else:
                a[i,j] = max(a[i-1,j],pricelist[i-1]+a[i-1,j-wlist[i-1]])
                # 如果不放->a[i-1,j],
                # 如果放-> 之前考虑放之前存好的最大重量相比
    print(a)

weights = [1,2,5,6,7,9]
price = [1,6,18,22,28,36]
solve(len(weights),13,weights,price)
[[ 0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  1  1  1  1  1  1  1  1  1  1  1  1  1]
 [ 0  1  6  7  7  7  7  7  7  7  7  7  7  7]
 [ 0  1  6  7  7 18 19 24 25 25 25 25 25 25]
 [ 0  1  6  7  7 18 22 24 28 29 29 40 41 46]
 [ 0  1  6  7  7 18 22 28 29 34 35 40 46 50]
 [ 0  1  6  7  7 18 22 28 29 36 37 42 46 50]]

2. 最长公共子序列

给定两个字符串str1和str2，返回两个字符串的最长公共子序列，例如：str1=\"1A2C3D4B56\",str2=\"B1D23CA45B6A\",\"123456\"和\"12C4B6\"都是最长公共子序列，返回哪一个都行。

分析：本题是非常经典的动态规划问题，假设str1的长度为M，str2的长度为N，则生成M*N的二维数组dp，dp[i][j]的含义是str1[0..i]与str2[0..j]的最长公共子序列的长度。

dp值的求法如下：

dp[i][j]的值必然和dp[i-1][j],dp[i][j-1],dp[i-1][j-1]相关，结合下面的代码来看，我们实际上是从第1行和第1列开始计算的，而把第0行和第0列都初始化为0，这是为了后面的取最大值在代码实现上的方便，dp[i][j]取三者之间的最大值。

def find_lcsubstr(s1, s2):
	# 下面4行不要直接写在循环中，减少计算
	s1_len = len(s1) + 1 					#为方便后续计算，多了1行1列
	s2_len = len(s2) + 1
	s3_len = len(s1)
	s4_len = len(s2)
	m = [[0 for j in range(s2_len)] for i in range(s1_len)] #生成0矩阵
	maxNum = 0   							#初始最长匹配长度
	p = 0  									#匹配的起始位置
	for i in range(s3_len):
		for j in range(s4_len):
			if s1[i] == s2[j]:				  #相同则累加
				m[i + 1][j + 1] = m[i][j] + 1 #给相同字符赋值，值为左上角值加1
				if m[i + 1][j + 1] > maxNum:
					maxNum = m[i + 1][j + 1]  #获取最大匹配长度
					p = i + 1 				  #记录最大匹配长度的终止位置
	print(m)
	return s1[p - maxNum : p], maxNum   	  #返回最长子串及其长度

3. 最长子回文串

Example 1:

Input: s = \"babad\"
Output: \"bab\"
Explanation: \"aba\" is also a valid answer.

Example 2:

Input: s = \"cbbd\"
Output: \"bb\"

思路与方法

如果一个子串是回文串，并且长度大于2，那么将他首位字母去掉之后依然是一个回文串，例如ababa,去掉之后bab是回文的。根据这样的思路，我们就可以用动态规划的方法解决本题。我们用 P[i,j]表示字符串P的子串

\\[p(i,j)=\\begin{cases} true，如果子串S_i....S_j是回文串\\\\ false， 其他情况\\end{cases}
\\]

这里的其他情况包含两种：

\\[s[i,j]本身不是回文串，以及\\quad i>j
\\]

那么我们就可以写出动态规划的状态转移方程：

\\[P(i,j)=P(i+1,j−1)∧(S_i
​
==S _j
​
)
\\]

意思就是只有当弃掉两边Si和Sj是回文串，并且首尾字母依然相等，则更大子串也是回文串。

\\[\\begin{cases} p(i,i)=true\\\\ p(i,j)=(S_i==S_j)\\quad j=i+1\\end{cases}
\\]

注意：在状态转移方程中，我们是从长度较短的字符串向长度较长的字符串进行转移的，因此一定要注意动态规划的循环顺序。

class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        if n < 2:
            return s

        max_len = 1
        begin = 0
        # dp[i][j] 表示 s[i..j] 是否是回文串
        dp = [[False] * n for _ in range(n)]
        for i in range(n):
            dp[i][i] = True

        # 递推开始
        # 先枚举子串长度
        for L in range(2, n + 1):
            # 枚举左边界，左边界的上限设置可以宽松一些
            for i in range(n):
                # 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                j = L + i - 1
                # 如果右边界越界，就可以退出当前循环
                if j >= n:
                    break

                if s[i] != s[j]:
                    dp[i][j] = False
                else:
                    if j - i < 3:
                        dp[i][j] = True
                    else:
                        dp[i][j] = dp[i + 1][j - 1]

                # 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if dp[i][j] and j - i + 1 > max_len:
                    max_len = j - i + 1
                    begin = i
        return s[begin:begin + max_len]



s = Solution()
ans = s.longestPalindrome(\"abcdeed\")
print(ans)

本文来自博客园，作者：ivanlee717，转载请注明原文链接：https://www.cnblogs.com/ivanlee717/p/17268425.html

来源：https://www.cnblogs.com/ivanlee717/p/17268425.html
本站部分图文来源于网络，如有侵权请联系删除。

未经允许不得转载：百木园 » 经典动态规划题（python）
标签：

相关推荐

  • 暂无文章

热门文章