封面图作者:Maxime Bourgeois
教程作者:SA九五二七
交作业:#优设每日作业#

此教程属于中阶教程,需要对AI的3D功能有一定的使用基础和了解,新手建议先看下面关于AI的3d功能基础讲解:
首先让大家直观感受一下不定向轴测图的含义:
原作者的原图为最常规的等角轴测图。
在临摹了作者的原图之后,我用不定向轴测图选择了一个向左的轴测角度进行了重新绘制,于是,它就会变成如下图向左倾斜的正方体。

然后我再选择一个朝右方的轴测图角度重新绘制。

它就会变成如上图的效果。
我们总结规律,传统轴测图都是用3d功能中的等角角度来绘制,我将为大家讲解的是任意角度轴测图的绘制方法,难度不是很大,只要找到三个基准面,然后根据基准面来绘制,就会变得很轻松。
以下文章分为两个部分,第一部分讲解AI-3D功能角度轴线的原理,第二部分根据原理如何找到轴测图中的三个面的基轴角度。
首先来讲解原理部分~
在讲原理之前我们先要明白两个概念。
在空间中相互垂直的三个轴线X、Y、Z,它们所组成的区域为三维空间,其中X、Y、Z相对于空间是不变的。
如下图:
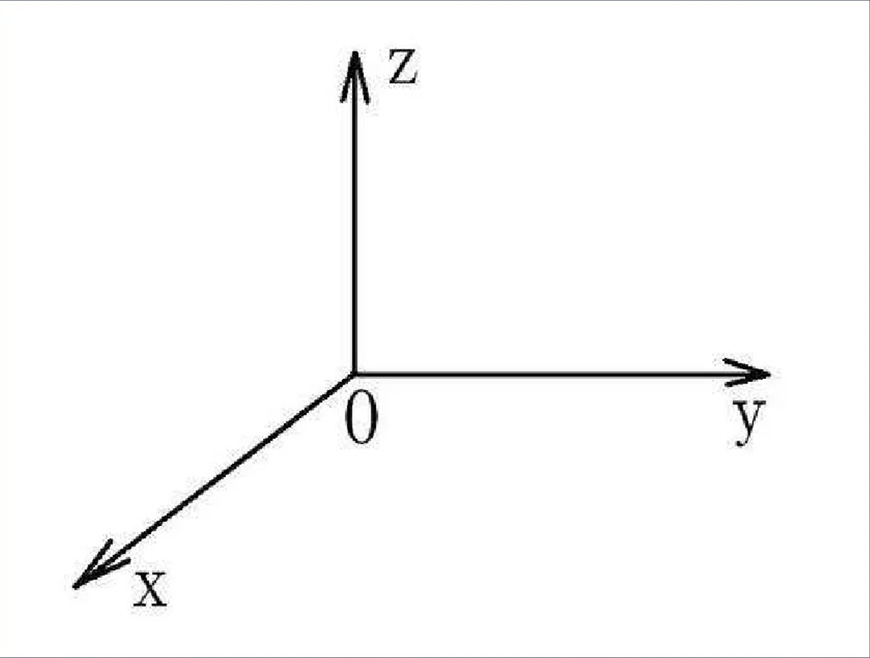
在AI的3D功能中也有三个轴线,每个轴线也有自己的旋转角度。
但是它们不同于空间坐标轴相对不变,它们的轴线会根据其他轴线角度的变换而发生改变,这里我把它们命名为角度坐标轴,以下文章中所讲的就是角度坐标轴。

3D功能中的立方体旁边有三个角度轴,我们从上至下给它们分别命名为:X轴、Y轴、Z轴,它们跟空间坐标轴很类似,但是不是同一个东西,这里需要注意。
经我研究发现,三根轴线并不是固定不动的,而是会随着角度轴变化而产生相应的变化。
X轴、Y轴、Z轴的轴线是基轴绑定制的关系,也就是说,X轴的轴线是绑定在Y轴上,Y轴的轴线绑定在Z轴上,只有Z轴的轴线是固定在垂直屏幕上不动的。
下面我来举例说一下这个关系的含义。

首先我们将三个轴上的角度都调整为0°,然后再将X轴上旋转30°。
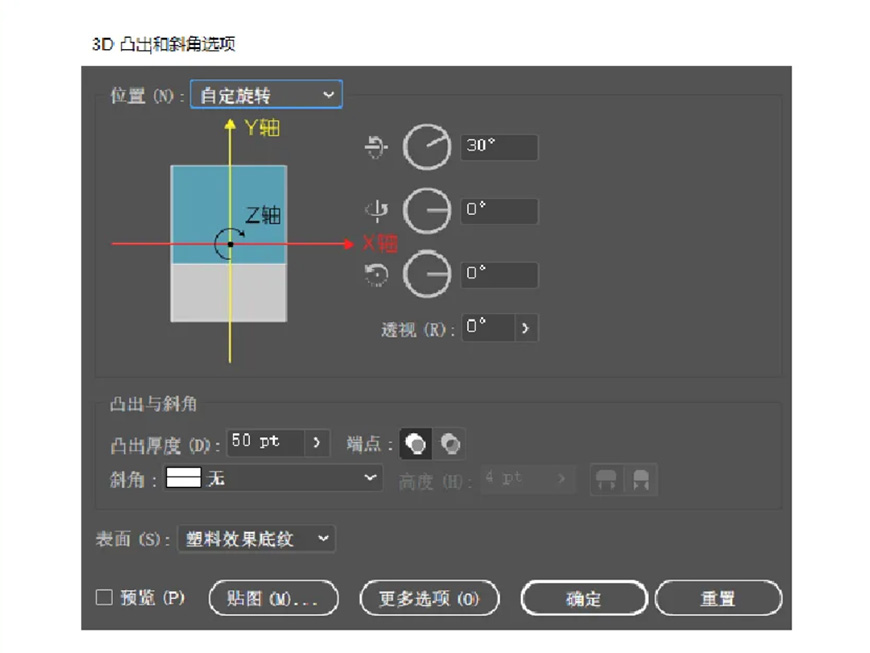
我们会发现物体按X轴旋转了30°。
接着我们将其他角度调整为0°,把Z轴调成30°。
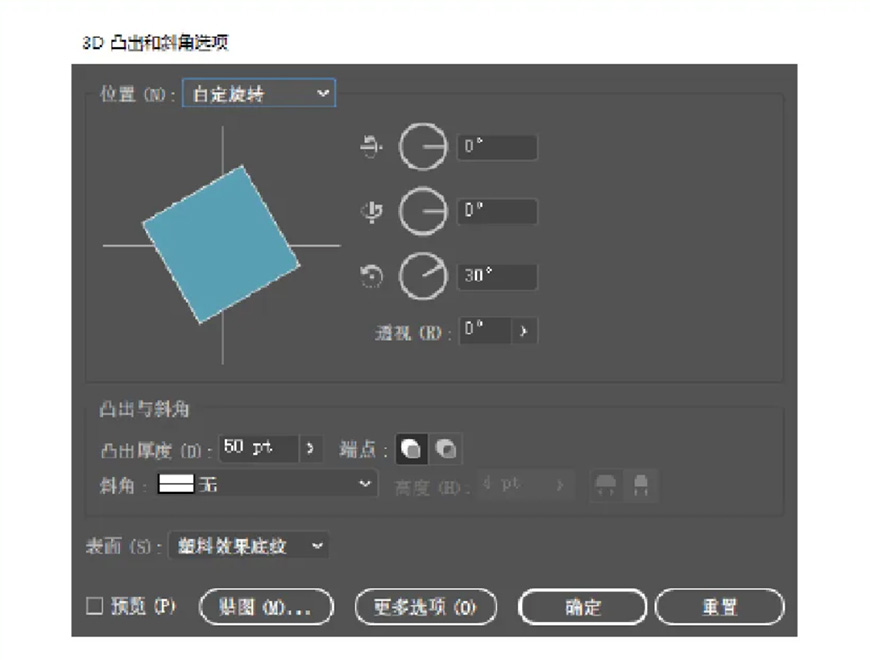
然后再将X轴也调整为30°,我们会发现物体旋转的方向已经不是水平的了,而是按照Z轴旋转了30°之后的角度,也就是下图中X轴的轴线旋转的。
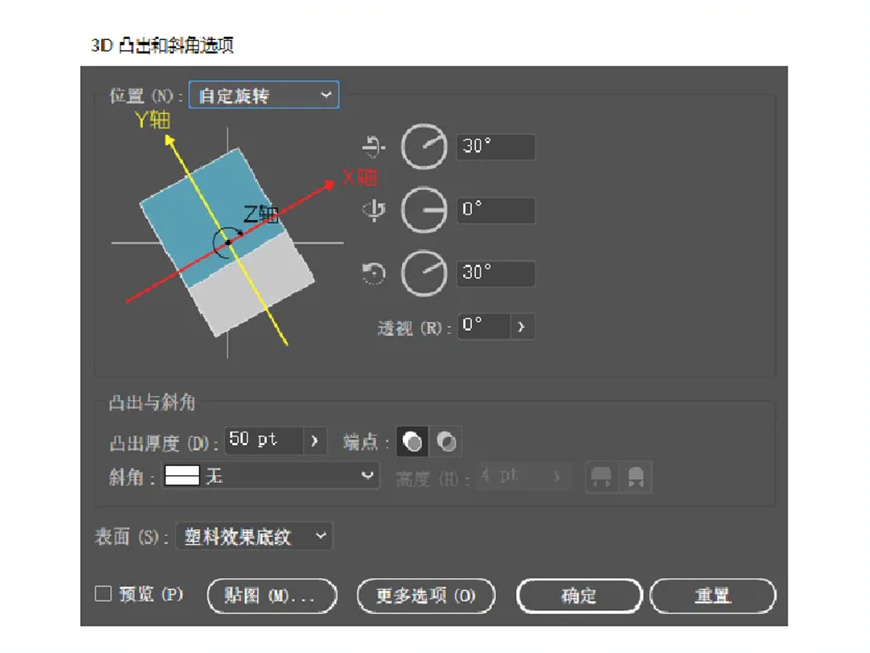
此时,如果给Y轴一定的角度,X的轴线还会发生一定变化,只是X轴始终垂直于Y轴,图片无法展示出钙效果,大家可以自行脑补脑补。
以上就是基轴绑定制的原理,其实很简单,只是轴线会变化而已。
这种基轴绑定制的关系会产生一个同轴现象。
就是当Y轴旋转-90°时,X轴与Z轴都垂直于屏幕,此时旋转X轴和旋转Z轴的效果是一样的。

我们先将所有轴线角度调整为0°,然后把Y轴调整为-90°,然后再给X轴一个角度。

随后我们把X轴调整为0°,然后再给Z轴同样的角度,会发现物体旋转的角度是一致的。
因为此时X轴和Z轴已经移动到了一起,所以调整X轴的角度还是调整Z轴的角度都是一样的效果~
这里我就不多做赘述了,大家多试几次就能看出来端倪。
这个原理可能单纯看图文,理解上会有一些困难,这里给大家推荐了两个2.5d的教程,大家可以先练习一下,然后再接着看后续的教程。
了解了原理之后,我们将继续为大家介绍不定向轴测图的实用技巧。
我们在用3D功能做轴测图的时候,只要找到轴测图的三个基准面的角度就可以了。
基准面:空间坐标系中,由X轴和Y轴组成Z面,由X轴和Z轴组成Y面,由Y轴和Z轴组成X面。
三个基准面即可确定一个三维空间。
比如下面这个图形:

我们用等角角度来做轴测图的时候,首先找到它的三个角度对应的基准面。
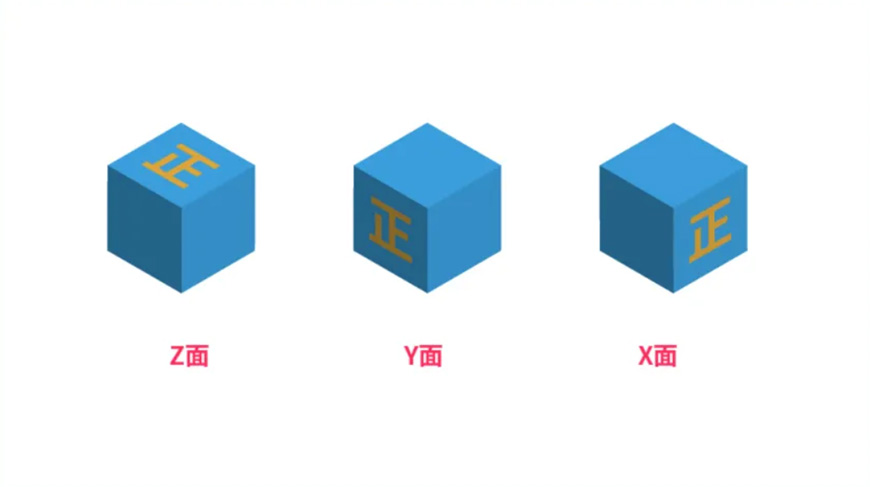
角度在坐标轴里分别为:

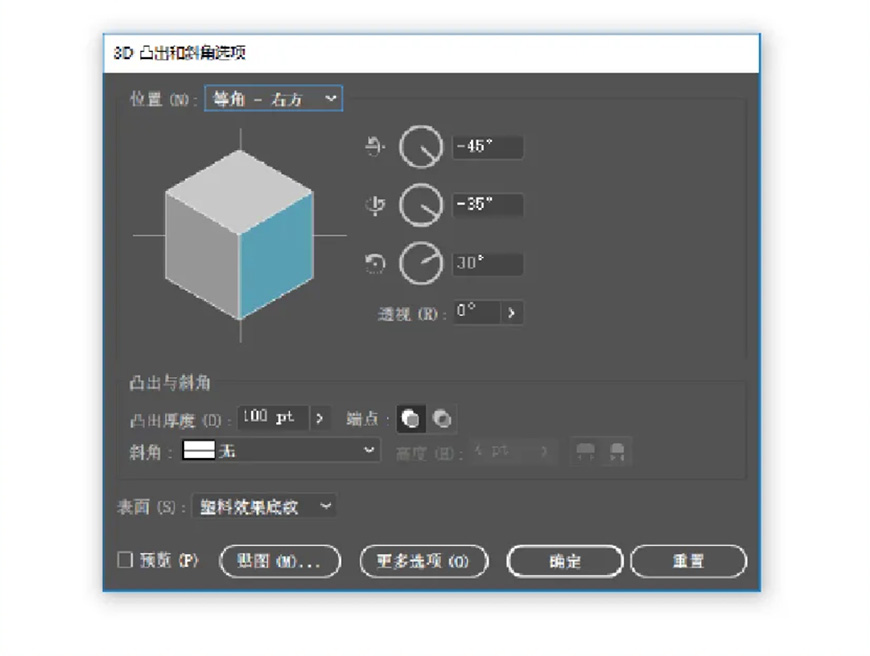
然后根据这三个基准面来作图,就能做出标准的轴测图了。

不定向轴测图只是基准面的角度有所不同,只要找到对应角度,画法是完全一样的~
这里,我们仍然用「正」来做例子。

首先,我们选定一个任意角度作为Z面。

Y面是最好找的一个面,只要将X轴的角度+或者-90°即可,如果X轴的角度大于0°就减去90°,如果X轴的角度小于0°就加上90°。

X面是最不好找的一个面,这里我们分成三小步来做。
第一步,复制一个Y面的图形,然后将Z轴角度调0°。
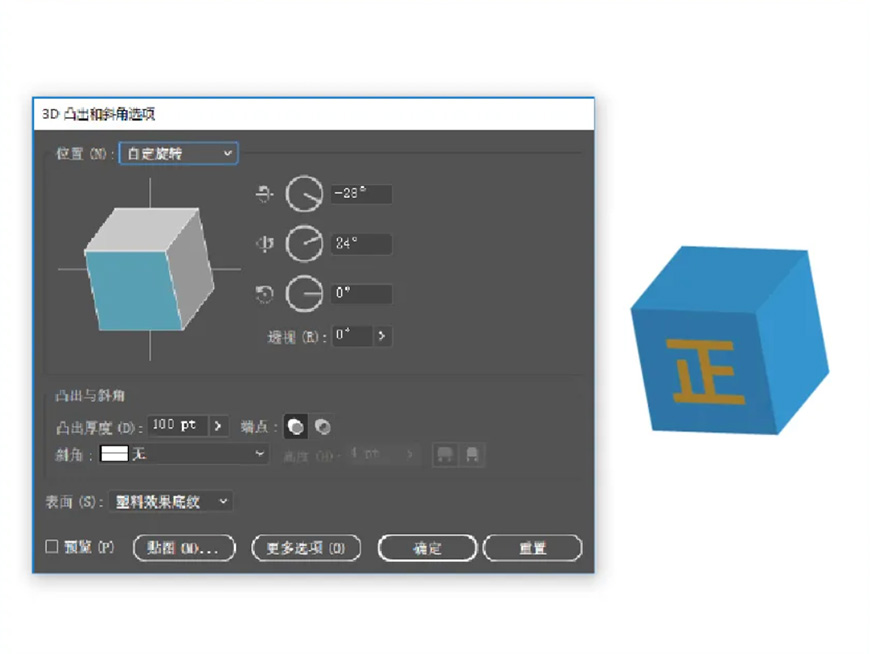
第二步,将3D选项中物体沿空间旋转90°。
只要顶部红色线段的地方看起来水平就可以了,会有误差,但是基本可以忽略不计。

第三步,将Z轴的角度加上刚才去掉的角度,我这里是-2°。

此时,我们不定向轴测图的三个基准面就都找好了。

之后作图只要根据这三个基准面来绘制就可以了,就比如我开篇做的例子。

上图为向左倾斜的2.5D轴测图。

我们再做一个向右侧倾斜的轴测图。
我们心里想做哪个角度,就可以做出哪个角度的轴测图,这样,我们就可以随心所欲地画图啦~

来源:https://uiiiuiii.com/illustrator/1212280644.html
图文来源于网络,如有侵权请联系删除。
 百木园
百木园