箱图简介

箱型图是一种用作显示一组数据分布情况的统计图，因型状如箱子而得名。
1977年由美国著名统计学家约翰·图基（John Tukey）发明。它能显示出一组数据的最大值、最小值、中位数及上下四分位数。

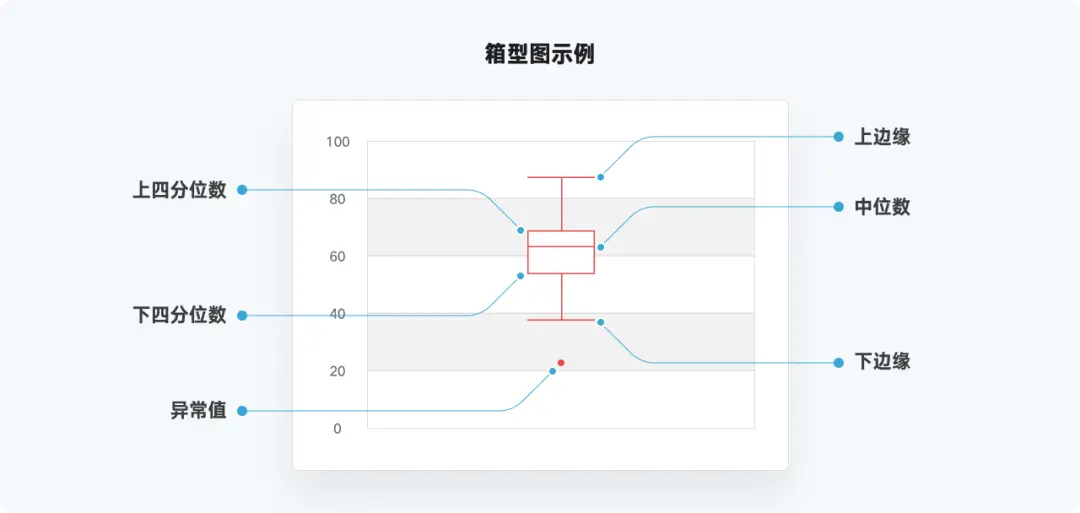
其中，中位数（50%），上四分位数（75%）和下四分位数（25%）都很好理解。
上边缘和下边缘的概念是不确定的，一般有以下几种情况（不限于以下几种情况）：

至于异常值，也就是比上边缘大，比下边缘小的值，如果上下边缘是左右数据中的最大值和最小值，那么就不会有异常值。

数据预处理中的箱图

箱图最大的优势是以一种简单的方式显示了数据的分布情况。
而我们在数据预处理之前，整体上了解数据各个特征的分布情况是非常有必要的，通过箱图，了解数据的质量。
比如：

了解数据各个特征（也就是每列）的质量和分布情况，有助于后续决策如何清洗数据，如何选择合适的算法来分析不同的特征。

示例

最后，通过一个简单的实例来演示如何通过箱图来检验数据的情况的。
数据来源：国家统计局历年粮食产量的统计数据。
​

数据比较多，这里为了演示，只取了3列来作图。

中稻和一季晚稻单位面积产量(公斤/公顷)
亚麻单位面积产量(公斤/公顷)
其他谷物单位面积产量(公斤/公顷)
冬小麦单位面积产量(公斤/公顷)
双季晚稻单位面积产量(公斤/公顷)
夏收粮食单位面积产量(公斤/公顷)
大豆单位面积产量(公斤/公顷)
大麦单位面积产量(公斤/公顷)
大麻单位面积产量(公斤/公顷)
小麦单位面积产量(公斤/公顷)
早稻单位面积产量(公斤/公顷)
春小麦单位面积产量(公斤/公顷)
棉花单位面积产量(公斤/公顷)
油料单位面积产量(公斤/公顷)
油菜籽单位面积产量(公斤/公顷)
烟叶单位面积产量(公斤/公顷)
烤烟单位面积产量(公斤/公顷)
玉米单位面积产量(公斤/公顷)
甘蔗单位面积产量(公斤/公顷)
甜菜单位面积产量(公斤/公顷)
秋粮单位面积产量(公斤/公顷)
稻谷单位面积产量(公斤/公顷)
粮食单位面积产量(公斤/公顷)
糖料单位面积产量(公斤/公顷)
红小豆单位面积产量(公斤/公顷)
绿豆单位面积产量(公斤/公顷)
胡麻籽单位面积产量(公斤/公顷)
芝麻单位面积产量(公斤/公顷)
花生单位面积产量(公斤/公顷)
苎麻单位面积产量(公斤/公顷)
葵花籽单位面积产量(公斤/公顷)
蔬菜单位面积产量(公斤/公顷)
薯类单位面积产量(公斤/公顷)
谷子单位面积产量(公斤/公顷)
谷物单位面积产量(公斤/公顷)
豆类单位面积产量(公斤/公顷)
马铃薯单位面积产量(公斤/公顷)
高粱单位面积产量(公斤/公顷)
麻类单位面积产量(公斤/公顷)
黄红麻单位面积产量(公斤/公顷)

前3列数据如下：

print(data)

​

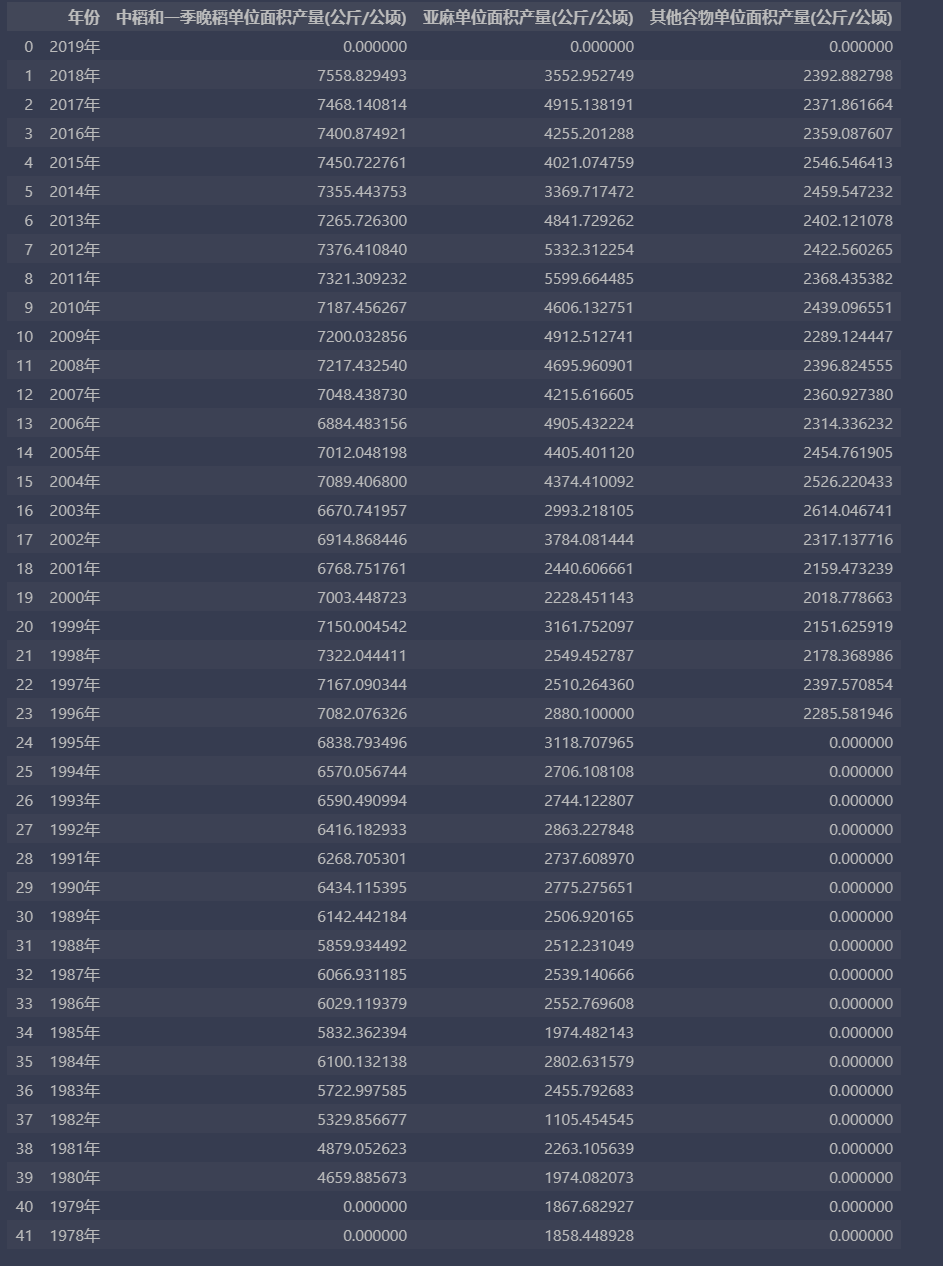
根据3个特征箱图如下：

box1, box2, box3 = data[\"中稻和一季晚稻单位面积产量(公斤/公顷)\"], data[\"亚麻单位面积产量(公斤/公顷)\"], data[\"其他谷物单位面积产量(公斤/公顷)\"]

plt.title(\"sample for 箱图\")
labels = [\"中稻和一季晚稻\", \"亚麻\", \"其他谷物\"]

plt.boxplot([box1, box2, box3], labels=labels)
plt.show()

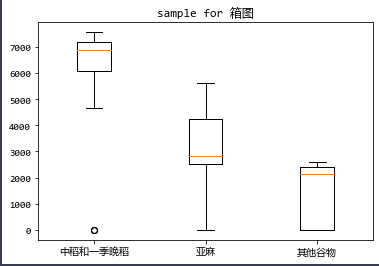
从图中可以看出，其他谷物的数据分布比较平均，而中稻和一季晚稻的数据偏重于上半部，亚麻的数据没有明显的偏重。
此外，只有一个异常值（中稻和一季晚稻的零值数据）。
​

箱图的默认上下边缘数据是 Q3 + whis(Q3-Q1) 和 Q1 - whis(Q3-Q1)，其中 whis = 1.5
我们可以通过调整 whis 的大小来调整上下边缘的值，比如：

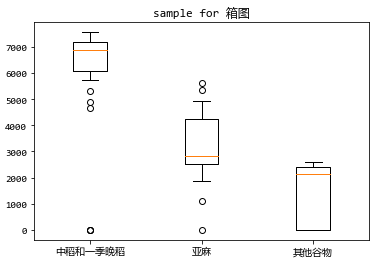
plt.boxplot([box1, box2, box3], labels=labels, whis=0.5)

这里 whis 设置为0.5，缩小了上下边缘的间距，异常值就增多了。

总结

通过箱图，可以直观看出整个数据中各个特征的分布情况。
在数据预处理之前，用来了解收集数据的概况大有帮助。

来源：https://www.cnblogs.com/wang_yb/p/15934262.html
图文来源于网络，如有侵权请联系删除。