JavaScript算法——排序算法 下

希尔排序

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
它与插入排序的不同之处在于，它会优先比较距离较远的元素。

希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列，分别进行直接插入排序，待整个序列中的记录\"基本有序\"时，再对全体记录进行依次直接插入排序。
分割排序目的：一步步让数字离自己正确的位置更近一点

• 实现步骤
  1.选择一个增量序列 t1，t2，……，tk，其中 ti > tj（递减至1）, tk = 1；
  2.按增量序列个数 k，对序列进行 k 趟排序；
  3.每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
• 实现图
  

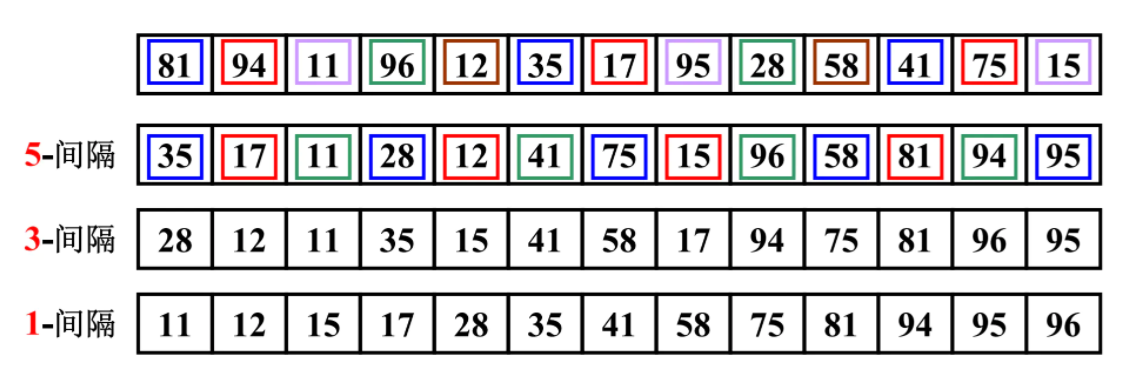
代码实现

// 希尔排序
function hillSort(array){
    let length = array.length;
    // 如果不是数组或者数组长度小于1 直接返回，不需要排序
    if(!Array.isArray(array) || length <= 1)return;
    //第一层确定增量的大小，每次增量的大小减半
    for (let gap = parseInt(length >> 1);gap >= 1; gap = parseInt(gap >> 1))
    {
        // 对每个分组使用插入排序，相当于将插入排序的1换成了 n
        for (let i = gap; i< length ;i++){
            let temp = array[i];//待排序数
            let j = i;
            while (j- gap >= 0 && array[j - gap] > temp){
                array [j] = array[j - gap];
                j -= gap;
            }
            array[j] = temp;//待排序数插到小于它的数后面
        }
    }
    return array;
}

堆排序

堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：
1.大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列
2.小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列

将数组看成一个完全二叉树，对于该完全二叉树只需要遍历一半的值，进行循环比对，把最大的结点赋值到根的位置，然后把根部的值和最后一个数值交换，排除最后一个数值继续打造大顶堆，最终形成一个小顶堆的算法。

• 设某结点序号为 i ,则其父结点为⌊ i /2⌋，2i为左子结点序号，2i+1为右子结点序号。其中，⌊⌋为向下取整符号。
• 当存储了n个元素时，⌊n/2⌋+1、⌊n/2⌋+1、···、n为叶结点。

// 创建堆，其实是对data数组做一个结构调整，使其具有堆的特性
function buildHeap(data) {
    var len = data.length;
    for(var i=Math.floor(len/2); i>=0; i--) {
        heapAjust(data, i, len);
    }
}
// 堆调整函数，即调整当前data为大根堆
function heapAjust(data, i, len) {
    var child = 2*i + 1;
    // 如果有孩子结点，默认情况是左孩子
    while(child <= len) {
        var temp = data[i];
        // 如果右孩子存在且其值大于左孩子的值，则将child指向右孩子
        if(child + 1 <= len && data[child] < data[child + 1]) {
            child = child + 1;
        }
        // 如果当前结点的值小于其孩子结点的值，则交换，直至循环结束
        if(data[i] < data[child]) {
            data[i] = data[child];
            data[child] = temp;
            i = child;
            child = 2*i + 1
        }else {
            break
        }
    }
}
// 排序
function heapSort(data) {
    var data = data.slice(0);
    if(!(data instanceof Array)) {
        return null;
    }
    if(data instanceof Array && data.length == 1) {
        return data;
    }
    // 将data数组改造为“堆”的结构
    buildHeap(data);

    var len = data.length;
    // 下面需要注意的时候参数的边界，参考文档里面程序中i的值是不对的
    for(var i=len-1; i>=0; i--) {
        swap(data, i, 0);
        heapAjust(data, 0, i-1);
    }
    return data;
}

计数排序

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。
作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
计数排序是分布式排序方法。分布式排序使用已组织好的辅助数据结构（称为桶），然后进行合并，得到排好序的数组。
计数排序使用一个用来存储每个元素在原始数组中出现次数的临时数组。在所有元素都计数完成后，临时数组已排好序并可迭代以构建排序后的结果数组。
它是用来排序整数的优秀算法（它是一个整数排序算法），时间复杂度为O(n+k)，其中k是临时计数数组的大小；但是，它确实需要更多的内存来存放临时数组。

function countingSort(arr, maxValue) {
    var bucket = new Array(maxValue+1),
        sortedIndex = 0;
        arrLen = arr.length,
        bucketLen = maxValue + 1;

    for (var i = 0; i < arrLen; i++) {
        if (!bucket[arr[i]]) {
            bucket[arr[i]] = 0;
        }
        bucket[arr[i]]++;
    }

    for (var j = 0; j < bucketLen; j++) {
        while(bucket[j] > 0) {
            arr[sortedIndex++] = j;
            bucket[j]--;
        }
    }

    return arr;
}

桶排序

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。
为了使桶排序更加高效，我们需要做到这两点：
1.在额外空间充足的情况下，尽量增大桶的数量
2.使用的映射函数能够将输入的N个数据均匀的分配到K个桶中
同时，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

• 什么时候最快（Best Cases）：
  当输入的数据可以均匀的分配到每一个桶中

• 什么时候最慢（Worst Cases）：
  当输入的数据被分配到了同一个桶中

• 代码实现：

function bucketSort(arr, bucketSize) {
    if (arr.length === 0) {
      return arr;
    }

    var i;
    var minValue = arr[0];
    var maxValue = arr[0];
    for (i = 1; i < arr.length; i++) {
      if (arr[i] < minValue) {
          minValue = arr[i];                //输入数据的最小值
      } else if (arr[i] > maxValue) {
          maxValue = arr[i];                //输入数据的最大值
      }
    }

    //桶的初始化
    var DEFAULT_BUCKET_SIZE = 5;            //设置桶的默认数量为5
    bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
    var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;   
    var buckets = new Array(bucketCount);
    for (i = 0; i < buckets.length; i++) {
        buckets[i] = [];
    }

    //利用映射函数将数据分配到各个桶中
    for (i = 0; i < arr.length; i++) {
        buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
    }

    arr.length = 0;
    for (i = 0; i < buckets.length; i++) {
        insertionSort(buckets[i]);                      //对每个桶进行排序，这里使用了插入排序
        for (var j = 0; j < buckets[i].length; j++) {
            arr.push(buckets[i][j]);                      
        }
    }

    return arr;
}

基数排序

基数排序有两种方法：
MSD 从高位开始进行排序
LSD 从低位开始进行排序

• 代码实现（LSD）：

// LSD Radix Sort
// 比较整型
var counter = [];

// 定义一个函数 arr待排序数组 maxDigit数组中最大数的位数，例如[1,10,100]的maxDigit为3
function radixSort(arr, maxDigit) {
    var mod = 10;
    var dev = 1;
    for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {

        // 把待排序的数组 arr 中的每一位整数，插入对应的容器
        for(var j = 0; j < arr.length; j++) {

            // 从个位开始，得到数组中每个数的每一位并保存在 bucket 变量中
            // bucket 变量的值可能为 0 1 2 3 4 5 6 7 8 9
            // 与之对应的 counter[bucket] 容器为 0 1 2 3 4 5 6 7 8 9
            var bucket = parseInt((arr[j] % mod) / dev);

            // 如果目前 bucket 变量的值对应的 counter[bucket] 容器还不存在（未初始化），则创建（初始化）一个新的空容器
            if(counter[bucket]==null) {
                counter[bucket] = [];
            }
            // 现在把这个 bucket 变量的值插入对应的 counter[bucket] 容器的尾部
            counter[bucket].push(arr[j]);
        }

        // 把 counter[bucket] 容器里的数依次取出 
        var pos = 0;
        for(var j = 0; j < counter.length; j++) {
            // 定义一个变量 value 用于保存conter[j].shift
            var value = null;
            if(counter[j]!=null) {
                while ((value = counter[j].shift()) != null) {
                      arr[pos++] = value;
                }
            }
        }
    }
    return arr;
}

• 基数排序 ， 计数排序 与桶排序的比较：
  这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：
  1.基数排序：根据键值的每位数字来分配桶
  2.计数排序：每个桶只存储单一键值
  3.桶排序：每个桶存储一定范围的数值

来源：https://www.cnblogs.com/starking-985/p/15966089.html
本站部分图文来源于网络，如有侵权请联系删除。