数据结构Java版Map&Set&搜索树-百木园

欢迎来访~

1.搜索

1.1概念及场景

1.2模型

2.Map 的使用

2.1 关于Map的说明

2.2 关于Map.Entry的说明,>

2.3 Map 的常用方法说明

3. Set 的说明

3.1常见方法说明

4.搜索树

4.1概念

4.2搜索树的查找

4.3搜索树的插入

4.4搜索树的删除

1.搜索

1.1概念及场景

①Map和Set的作用：

一种专门用来进行搜索的容器或者数据结构，其搜索的效率与其具体的实例化子类有关
。

②Map和Set相比于其他类型的优点：

之前我们学过的常见搜索方式有：
直接遍历，二分查找等

上述排序比较适合静态类型的查找，即一般不会对区间进行插入和删除操作了，而现实中的查找比如：

1. 根据姓名查询考试成绩

2.
通讯录，即根据姓名查询联系方式

3.
不重复集合，即需要先搜索关键字是否已经在集合中

可能在查找时进行一些插入和删除的操作，即动态查找，那上述两种方式就不太适合了，本节介绍的
Map
和
Set
是一种适合
动态查找的集合容器
。

1.2模型

1. 纯 key 模型：

eg.有一个英文词典，快速查找一个单词是否在词典中；快速查找某个名字在不在通讯录中

2.Key-Value 模型：

eg.统计文件中每个单词出现的次数，统计结果是每个单词都有与其对应的次数：<单词，单词出现的次数
> ;梁山好汉的江湖绰号：每个好汉都有自己的江湖绰号

而
Map中存储的就是key-value的键值对，Set中只存储了Key

2.Map 的使用

2.1 关于Map的说明

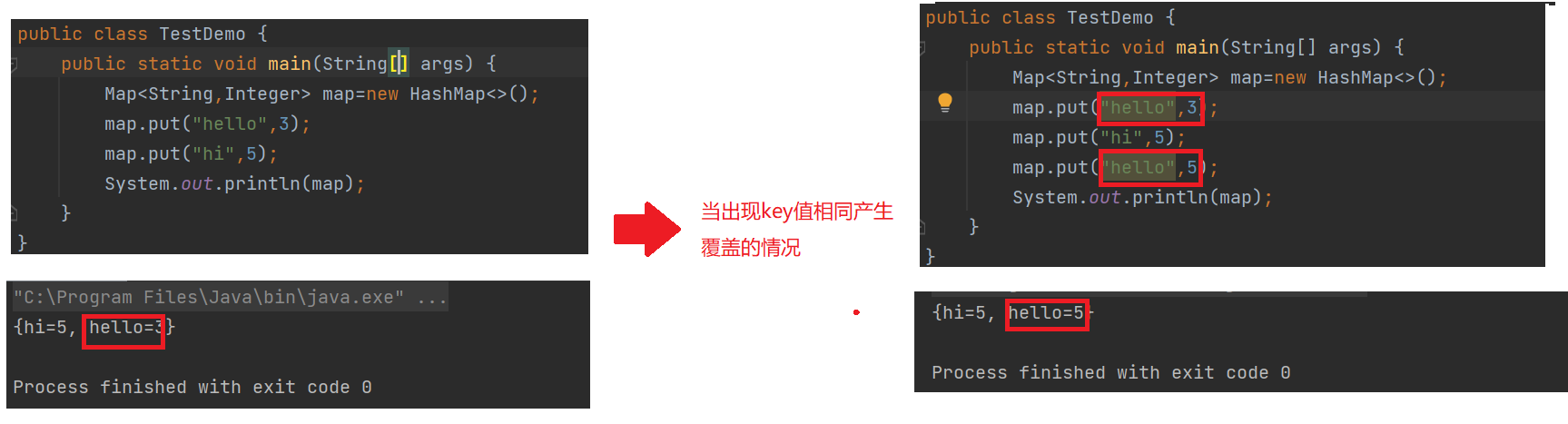
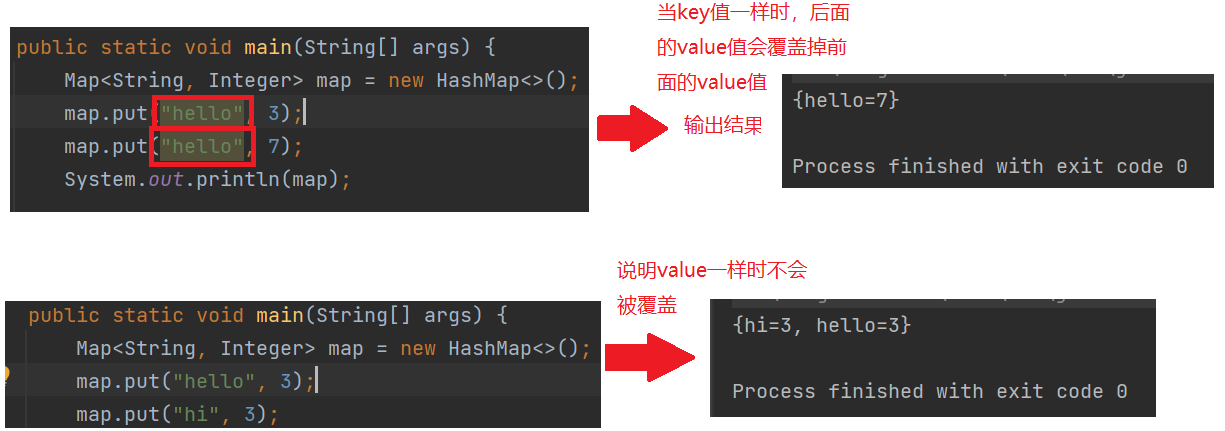
Map是一个接口类，该类没有继承自Collection，该类中存储的是<K,V>结构的键值对，并且K一定是唯一的，不能重复。（当后续出现重复的key值时，原来的value将会被替代）

解释图如下:（当后续出现重复的key值时，原来的value将会被替代）

2.2 关于Map.Entry<K, V>的说明

①内在结构：

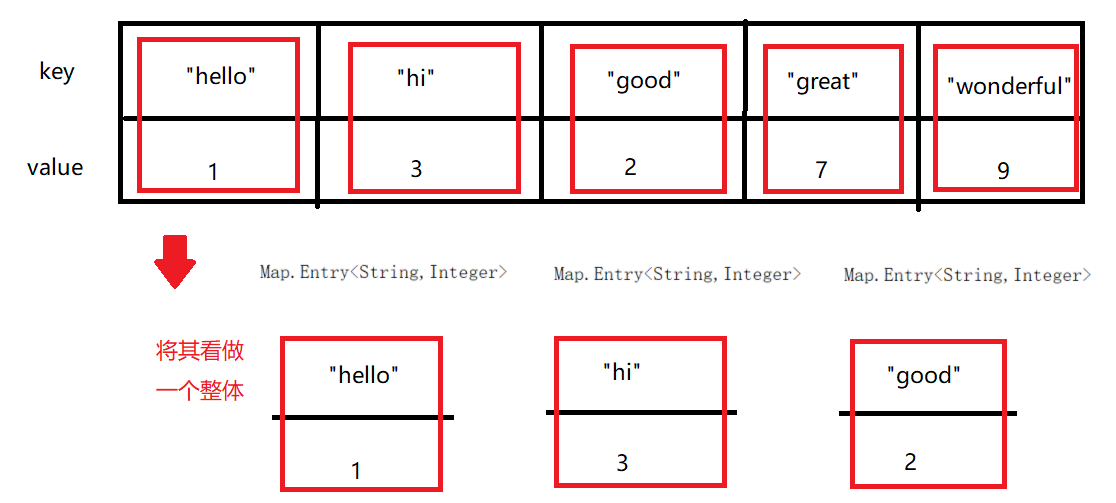
Map.Entry<K, V> 是Map内部实现的用来存放<key, value>键值对映射关系的内部类，该内部类中主要提供了 <key, value>的获取，value的设置以及Key的比较方式。

（将Map.Entry<K, V>中的<K,V>看作一个整体，来进行存储）

②常用方法

方法解释

K
getKey
()

返回
entry
中的
key

V
getValue
()

返回
entry
中的
value

V setValue(V value)

将键值对中的
value
替换为指定
value

2.3 Map 的常用方法说明

①常用方法说明：

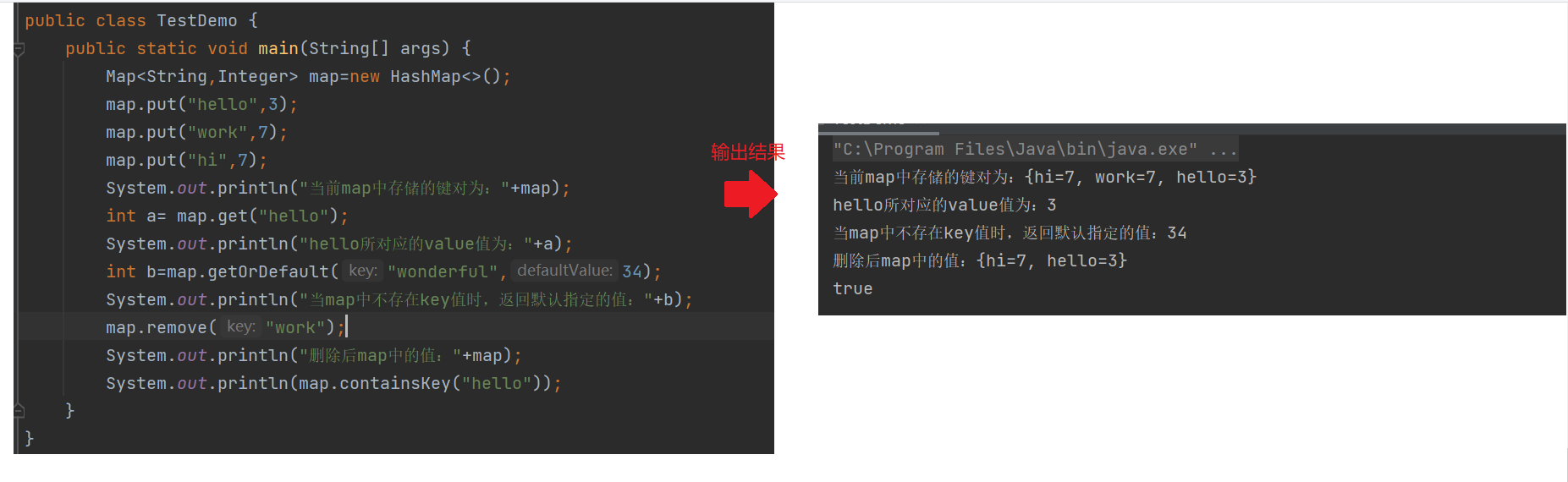
方法解释

V get(Object key) 返回 key 对应的 value

V getOrDefault(Object key, V defaultValue) 返回 key 对应的 value，key 不存在，返回默认值

V put(K key, V value) 设置 key 对应的 value

V remove(Object key) 删除 key 对应的映射关系

Set<K> keySet() 返回所有 key 的不重复集合

Collection<V> values() 返回所有 value 的可重复集合

Set<Map.Entry<K, V>> entrySet() 返回所有的 key-value 映射关系

boolean containsKey(Object key) 判断是否包含 key

boolean containsValue(Object value) 判断是否包含 value

②使用范例如下：

③注意事项：

a.Map是一个接口，不能直接实例化对象，如果要实例化对象只能实例化其实现类TreeMap或者HashMap

b.Map中存放键值对的Key是唯一的，value是可以重复的

c.在Map中插入键值对时，key不能为空，否则就会抛NullPointerException异常，但是value可以为空

d.Map中的value可以全部分离出来，存储在Collection的任何一个子集合中(value可能有重复)。

e.Map中键值对的Key不能直接修改，value可以修改，如果要修改key，只能先将该key删除掉，然后再来进行重新插入。

3. Set 的说明

Set与Map主要的不同有两点：Set是继承自Collection的接口类，Set中只存储了Key

3.1常见方法说明

①常用方法说明：

方法解释

boolean add(E e) 添加元素，但重复元素不会被添加成功

void clear() 清空集合

boolean contains(Object o) 判断 o 是否在集合中

Iterator<E> iterator() 返回迭代器

boolean remove(Object o) 删除集合中的 o

int size()
返回set中元素的个数

boolean isEmpty() 检测set是否为空，空返回true，否则返回false

Object[] toArray() 将set中的元素转换为数组返回

boolean containsAll(Collection<?> c) 集合c中的元素是否在set中全部存在，是返回true，否则返回false

boolean addAll(Collection<? extends

E> c)
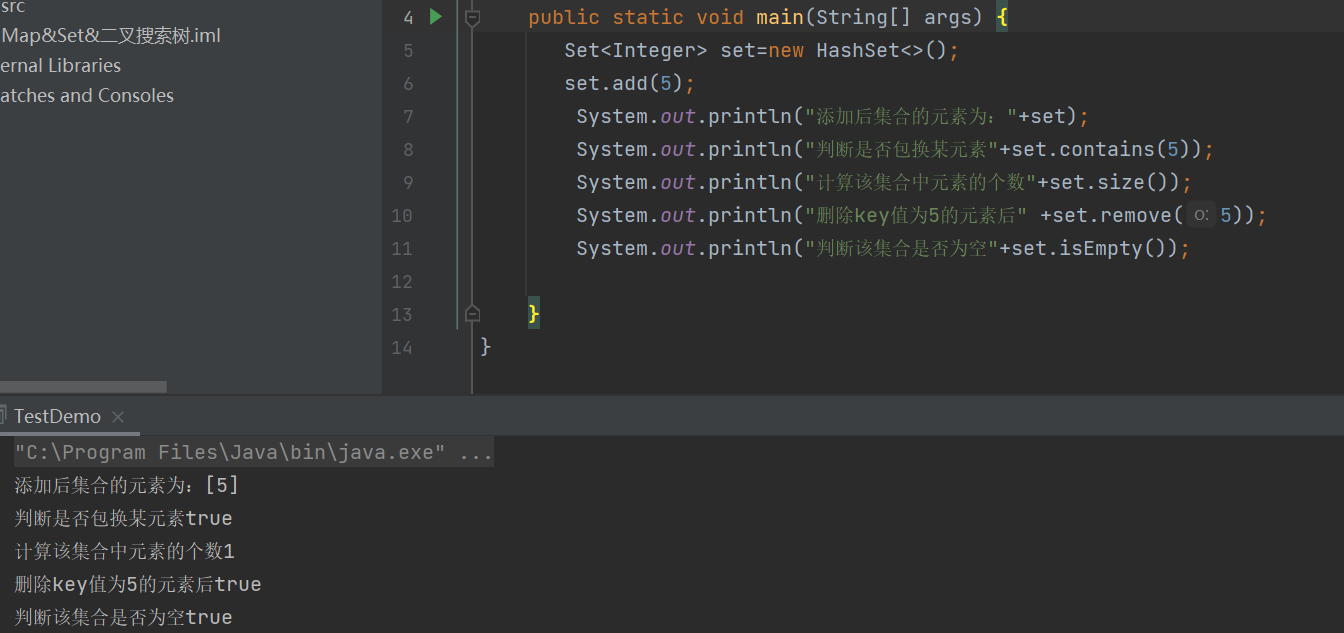
将集合c中的元素添加到set中，可以达到去重的效果

②使用范例如下：

③注意事项：

Set中只存储了key，并且要求key一定要唯一（与Map尤为不同的一点）

4.搜索树

4.1概念

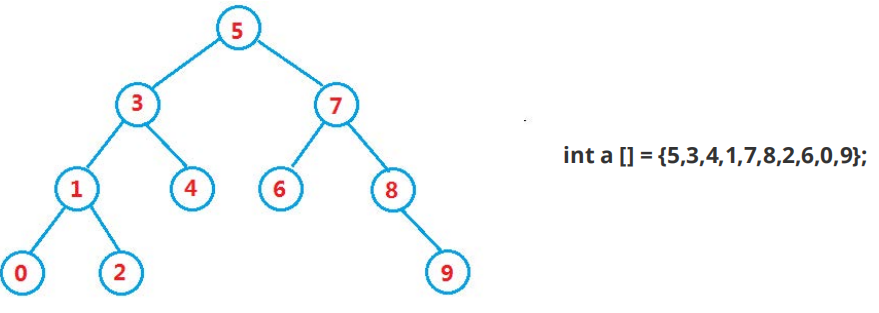
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

①如果它的左子树不为空，则左子树上所有节点的值都小于根节点的值

②如果它的右子树不为空，则右子树上所有节点的值都大于根节点的值

③它的左右子树也分别为二叉搜索树

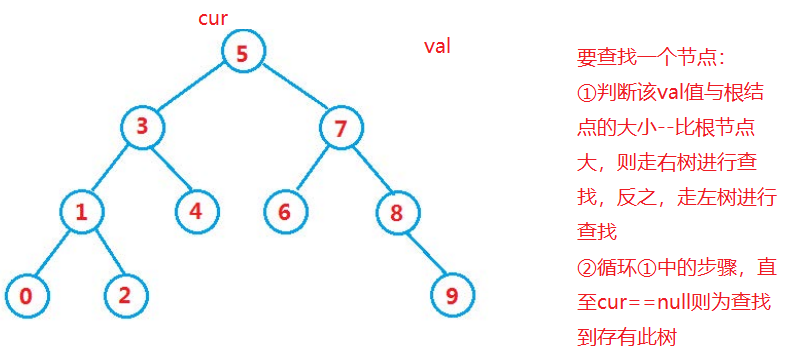
4.2搜索树的查找

解题思路：

代码如下：

//创建结点
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node(int val) {
        this.val = val;
    }
}

public class BinnarySearchTree {
    public Node root = null;
    public Node search(int value) {
        Node cur = root;
        while (cur != null) {
            if (cur.val < value) {
                cur = cur.right;
            } else if (cur.val == value) {
                return cur;
            } else {
                cur = cur.left;
            }
        }
        return null;//代表没有这个数据
    }

4.3搜索树的插入

解题思路：（与查找二叉树相似）

①查找到该根结点应该存储的位置

②存入该节点

代码如下：

  public boolean insert(int val) {
        if (root == null) {
            root = new Node(val);
            return true;
        }

        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if (cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else if (cur.val == val) {
                return false;//不能有相同的数据
            } else {
                parent = cur;
                cur = cur.left;
            }
        }
        Node node = new Node(val);
        if (parent.val < val) {
            parent.right = node;
        } else {
            parent.left = node;
        }
        return true;
    }

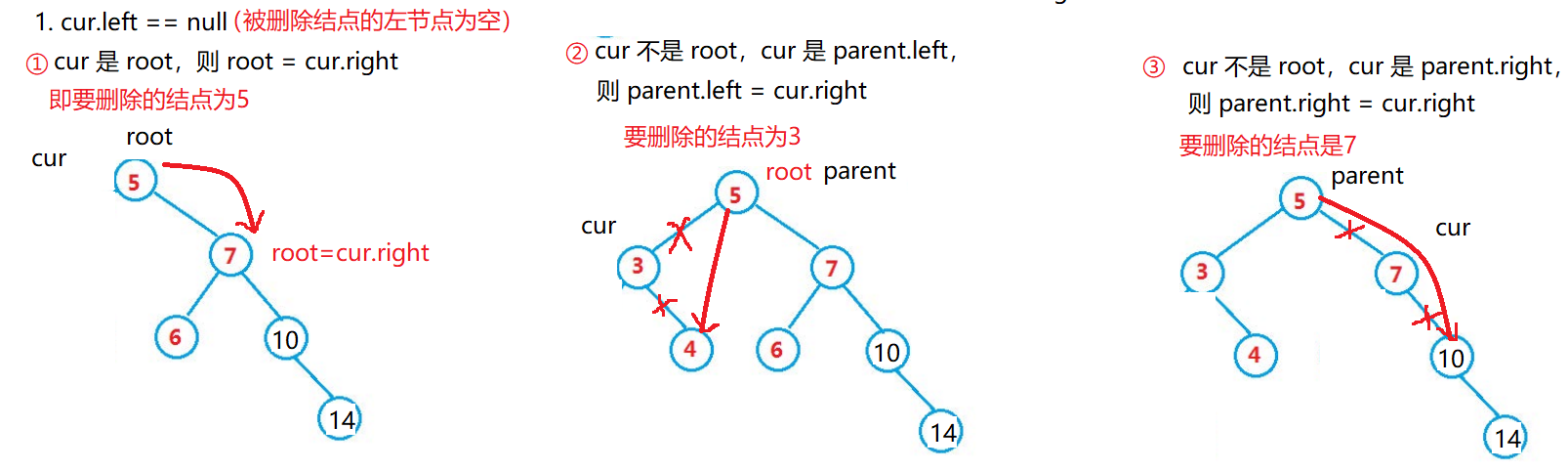
4.4搜索树的删除（难点）

解题思路：

1. cur.left == null

①cur
是
root
，则
root = cur.right

②cur
不是
root
，
cur
是
parent.left
，则
parent.left = cur.right

③cur
不是
root，
cur
是
parent.right
，则
parent.right = cur.right

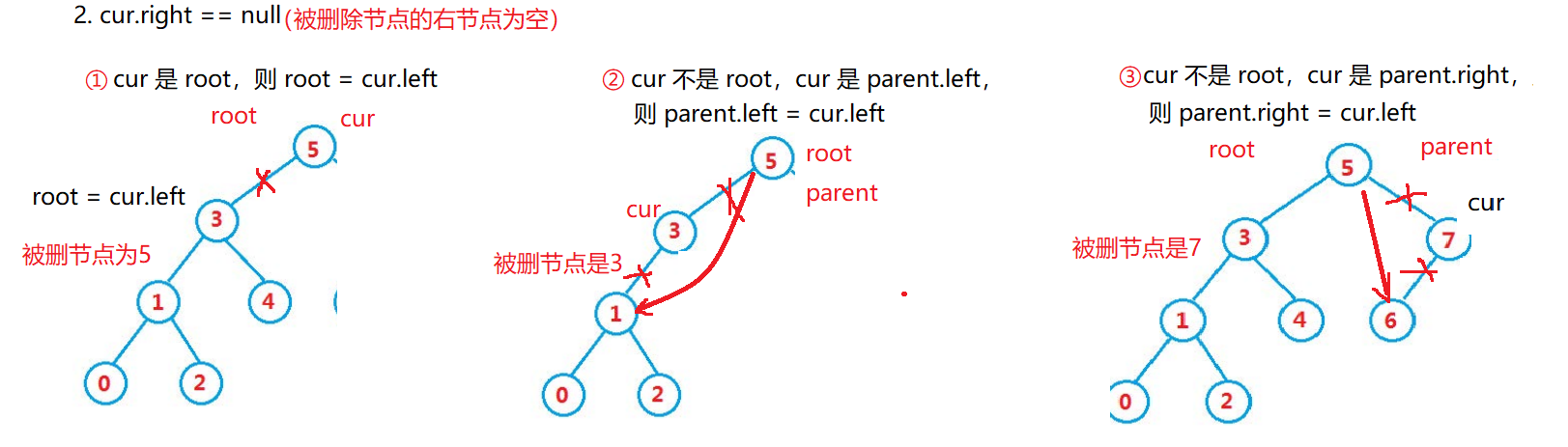
2.
cur.right == null

①cur
是
root
，则
root = cur.left

②cur
不是
root
，
cur
是
parent.left
，则
parent.left = cur.left

③cur
不是
root
，
cur
是
parent.right
，则
parent.right = cur.left

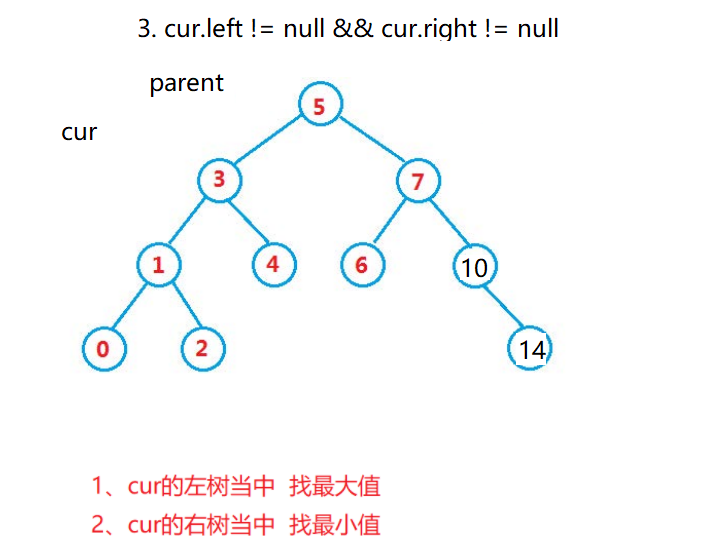
3. cur.left != null && cur.right != null（难点）

思路：
需要使用
替换法
进行删除，即在它的右子树中寻找中序下的第一个结点
(
关键码最小
)
，用它的值填补到被删除节点中，再来处理该结点的删除问题

整体代码如下:

//创建节点
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node(int val) {
        this.val = val;
    }
}
public void remove(int key) {
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                //这里开始删除
                removeNode(cur,parent);
                break;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }

    public void removeNode(Node cur,Node parent) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent = cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
//中序遍历
    public void inOrder(Node root) {
        if(root == null) return;
        inOrder(root.left);
        System.out.print(root.val+\" \");
        inOrder(root.right);
    }

感谢观看~

来源：https://blog.csdn.net/weixin_58850105/article/details/123290752
本站部分图文来源于网络，如有侵权请联系删除。

方法	解释
K getKey ()	返回 entry 中的 key
V getValue ()	返回 entry 中的 value
V setValue(V value)	将键值对中的 value 替换为指定 value

数据结构Java版Map&Set&搜索树

1.搜索

1.1概念及场景

1.2模型

2.Map 的使用

2.1 关于Map的说明

2.2 关于Map.Entry<K, V>的说明

2.3 Map 的常用方法说明

3. Set 的说明

3.1常见方法说明

4.搜索树

4.1概念

4.2搜索树的查找

4.3搜索树的插入

4.4搜索树的删除（难点）

相关推荐

热门文章

方法	解释
V get(Object key)	返回 key 对应的 value
V getOrDefault(Object key, V defaultValue)	返回 key 对应的 value，key 不存在，返回默认值
V put(K key, V value)	设置 key 对应的 value
V remove(Object key)	删除 key 对应的映射关系
Set<K> keySet()	返回所有 key 的不重复集合
Collection<V> values()	返回所有 value 的可重复集合
Set<Map.Entry<K, V>> entrySet()	返回所有的 key-value 映射关系
boolean containsKey(Object key)	判断是否包含 key
boolean containsValue(Object value)	判断是否包含 value

方法	解释
boolean add(E e)	添加元素，但重复元素不会被添加成功
void clear()	清空集合
boolean contains(Object o)	判断 o 是否在集合中
Iterator<E> iterator()	返回迭代器
boolean remove(Object o)	删除集合中的 o
int size()	返回set中元素的个数
boolean isEmpty()	检测set是否为空，空返回true，否则返回false
Object[] toArray()	将set中的元素转换为数组返回
boolean containsAll(Collection<?> c)	集合c中的元素是否在set中全部存在，是返回true，否则返回false
boolean addAll(Collection<? extends E> c)	将集合c中的元素添加到set中，可以达到去重的效果