一. 归并排序算法简介
归并排序算法是一种采用了分治策略的排序算法。它通过递归地先使每个子序列有序,再将两个有序的序列进行合并成一个有序的序列(也可以采用非递归的方式实现,效率更高一些)。归并算法是稳定和高效的排序算法(适用于复杂对象(结构体)数列的稳定排序)
二. 算法复杂度
最理想情况:O(nlogn)
最坏情况: O(nlogn)
三. 算法分治思路
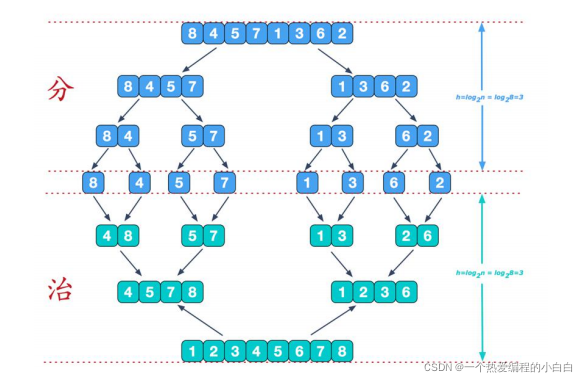
- 将数组切片为相同长度的两部分,长度为LEN的数组,分解为:两个子数组,一个是 nums[0...LEN/2] 另一个是 nums[LEN/2+1...LEN]
- 递归的对两个部分进行相同的切片操作,直到数组长度为1
- 对已经排好序的两个切片进行合并操作
四. 算法原理示意图
五. 算法实现
5.1 递归实现
package main
import (
\"fmt\"
)
func mergeSort1(array []int) []int {
arrLen := len(array);
if arrLen < 2 {
return array;
}
i := arrLen >>1;
leftSub := mergeSort1(array[0:i]);
rightSub := mergeSort1(array[i:]);
result := merge1(leftSub, rightSub);
return result;
}
func merge1(left []int, right []int) []int {
m := len(left);
n := len(right);
result := make([]int, m+n, m+n);
i, j, k := 0, 0, 0;
for i < m && j < n {
if left[i] <= right[j] {
result[k] = left[i];
k++;
i++;
} else {
result[k] = right[j];
k++;
j++;
}
}
if i == m {
for j < n {
result[k] = right[j];
k++;
j++;
}
}
if j == n {
for i < m {
result[k] = left[i];
k++;
i++;
}
}
return result;
}
5.2 非递归实现
//merge sort using no recursion
/****
// i: the begin index of old sub-array, j: the begin index of even sub-array
|<- k ->| |<- k ->| //case: k = 4
array [0,1,2,3] [4,5,6,7][8,9]
^ ^ ^
i j arrLen
****/
//merge sort using no recursion
func mergeSort2(array []int){
arrLen := len(array);
if arrLen <= 0 {
return;
}
list := make([]int, arrLen, arrLen);
source := &array;
target := &list;
flag := 0;
// k is the arrLength of sub-array,k=1,2,4,...
for k:= 1; k < arrLen; k <<=1 {
if flag == 1{
source = &list;
target = &array;
} else {
source = &array;
target = &list;
}
flag = 1 - flag;
//i, j is the begin index of sub-array
i, j := 0, k;
for n:= 0 ; n < arrLen; {
p, q:= i, j;
pEnd := i + k;
if pEnd > arrLen {
pEnd = arrLen;
}
qEnd := j + k;
if qEnd > arrLen {
qEnd = arrLen;
}
for (p < pEnd) && (q < qEnd) {
if (*source)[p] <= (*source)[q] {
(*target)[n] = (*source)[p];
n++;
p++;
} else {
(*target)[n] = (*source)[q];
n++;
q++;
}
}
//copy the left data of sub_array indexed by q
if p >= pEnd {
for q < qEnd {
(*target)[n] = (*source)[q];
n++;
q++;
}
}
//copy the left data of sub_array indexed by p
if q >= qEnd {
for p < pEnd {
(*target)[n] = (*source)[p];
n++;
p++;
}
}
i += k << 1;
j += k << 1;
}
}
if flag == 1 {
for r:=0; r < arrLen; r++ {
array[r] = list[r];
}
}
}
func main() {
arr := []int{9,4, 6, 8, 6, 30, 28, 2, 3, 50};
fmt.Println(arr);
sortArr := mergeSort1(arr);
fmt.Println(sortArr);
mergeSort2(arr);
fmt.Println(arr);
}
说明,递归算法容易理解,因为涉及到嵌套递归和临时空间开销,效率不高,在项目实践中不建议使用;非递归算法,采用自下向上从最小长度为1的子数组(子数组长度分别为:1,2,4,8,...直到大于原数组长度)开始归并,直到归并排序完成,效率很高,另外只申请了和原数组等长的临时空间用于存储中间归并结果,空间开销小。
来源:https://www.cnblogs.com/seaman9/p/16041206.html
本站部分图文来源于网络,如有侵权请联系删除。
 百木园
百木园