前言
回归分析就是用于预测输入变量(自变量)和输出变量(因变量)之间的关系,特别当输入的值发生变化时,输出变量值也发生改变!回归简单来说就是对数据进行拟合。线性回归就是通过线性的函数对数据进行拟合。机器学习并不能实现预言,只能实现简单的预测。我们这次对房价关于其他因素的关系。
波士顿房价预测
下载相关数据集
- 数据集是506行14列的波士顿房价数据集,数据集是开源的。
wget.download(url=\'https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data\',out= \'housing.data\')
wget.download(url=\'https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.names\',out=\'housing.names\')
wget.download(url=\'https://archive.ics.uci.edu/ml/machine-learning-databases/housing/Index\',out=\'Index\')
对数据集进行处理
feature_names = [\'CRIM\',\'ZN\',\'INDUS\',\'CHAS\',\'NOX\',\'RM\',\'AGE\',\'DIS\',\'RAD\',\'TAX\',\'PTRATIO\',\'B\',\'LSTAT\',\'MEDV\']
feature_num = len(feature_names)
print(feature_num)
# 把7084 变为506*14
housing_data = housing_data.reshape(housing_data.shape[0]//feature_num,feature_num)
print(housing_data.shape[0])
# 打印第一行数据
print(housing_data[:1])
## 归一化
feature_max = housing_data.max(axis=0)
feature_min = housing_data.min(axis=0)
feature_avg = housing_data.sum(axis=0)/housing_data.shape[0]
模型定义
## 实例化模型
def Model():
model = linear_model.LinearRegression()
return model
# 拟合模型
def train(model,x,y):
model.fit(x,y)
可视化模型效果
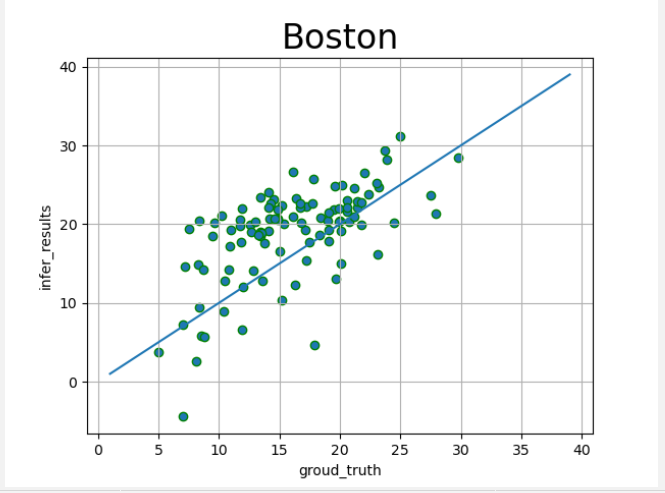
def draw_infer_result(groud_truths,infer_results):
title = \'Boston\'
plt.title(title,fontsize=24)
x = np.arange(1,40)
y = x
plt.plot(x,y)
plt.xlabel(\'groud_truth\')
plt.ylabel(\'infer_results\')
plt.scatter(groud_truths,infer_results,edgecolors=\'green\',label=\'training cost\')
plt.grid()
plt.show()
整体代码
## 基于线性回归实现房价预测
## 拟合函数模型
## 梯度下降方法
## 开源房价策略数据集
import wget
import numpy as np
import os
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import linear_model
## 下载之后注释掉
\'\'\'
wget.download(url=\'https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data\',out= \'housing.data\')
wget.download(url=\'https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.names\',out=\'housing.names\')
wget.download(url=\'https://archive.ics.uci.edu/ml/machine-learning-databases/housing/Index\',out=\'Index\')
\'\'\'
\'\'\'
1. CRIM per capita crime rate by town
2. ZN proportion of residential land zoned for lots over
25,000 sq.ft.
3. INDUS proportion of non-retail business acres per town
4. CHAS Charles River dummy variable (= 1 if tract bounds
river; 0 otherwise)
5. NOX nitric oxides concentration (parts per 10 million)
6. RM average number of rooms per dwelling
7. AGE proportion of owner-occupied units built prior to 1940
8. DIS weighted distances to five Boston employment centres
9. RAD index of accessibility to radial highways
10. TAX full-value property-tax rate per $10,000
11. PTRATIO pupil-teacher ratio by town
12. B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks
by town
13. LSTAT % lower status of the population
14. MEDV Median value of owner-occupied homes in $1000\'s
\'\'\'
## 数据加载
datafile = \'./housing.data\'
housing_data = np.fromfile(datafile,sep=\' \')
print(housing_data.shape)
feature_names = [\'CRIM\',\'ZN\',\'INDUS\',\'CHAS\',\'NOX\',\'RM\',\'AGE\',\'DIS\',\'RAD\',\'TAX\',\'PTRATIO\',\'B\',\'LSTAT\',\'MEDV\']
feature_num = len(feature_names)
print(feature_num)
# 把7084 变为506*14
housing_data = housing_data.reshape(housing_data.shape[0]//feature_num,feature_num)
print(housing_data.shape[0])
# 打印第一行数据
print(housing_data[:1])
## 归一化
feature_max = housing_data.max(axis=0)
feature_min = housing_data.min(axis=0)
feature_avg = housing_data.sum(axis=0)/housing_data.shape[0]
def feature_norm(input):
f_size = input.shape
output_features = np.zeros(f_size,np.float32)
for batch_id in range(f_size[0]):
for index in range(13):
output_features[batch_id][index] = (input[batch_id][index]-feature_avg[index])/(feature_max[index]-feature_min[index])
return output_features
housing_features = feature_norm(housing_data[:,:13])
housing_data = np.c_[housing_features,housing_data[:,-1]].astype(np.float32)
## 划分数据集 8:2
ratio =0.8
offset = int(housing_data.shape[0]*ratio)
train_data = housing_data[:offset]
test_data = housing_data[offset:]
print(train_data[:2])
## 模型配置
## 线性回归
## 实例化模型
def Model():
model = linear_model.LinearRegression()
return model
# 拟合模型
def train(model,x,y):
model.fit(x,y)
## 模型训练
X, y = train_data[:,:13], train_data[:,-1:]
model = Model()
train(model,X,y)
x_test, y_test = test_data[:,:13], test_data[:,-1:]
prefict = model.predict(x_test)
## 模型评估
infer_results = []
groud_truths = []
def draw_infer_result(groud_truths,infer_results):
title = \'Boston\'
plt.title(title,fontsize=24)
x = np.arange(1,40)
y = x
plt.plot(x,y)
plt.xlabel(\'groud_truth\')
plt.ylabel(\'infer_results\')
plt.scatter(groud_truths,infer_results,edgecolors=\'green\',label=\'training cost\')
plt.grid()
plt.show()
draw_infer_result(y_test,prefict)
效果展示
总结
线性回归预测还是比较简单的,可以简单理解为函数拟合,数据集是使用的开源的波士顿房价的数据集,算法也是打包好的包,方便我们引用。
来源:https://www.cnblogs.com/hjk-airl/p/16405474.html
本站部分图文来源于网络,如有侵权请联系删除。
 百木园
百木园