【机器学习】K-means聚类分析-百木园

前言

聚类问题是无监督学习的问题，算法思想就是物以类聚，人以群分，聚类算法感知样本间的相似度，进行类别归纳，对新输入进行输出预测，输出变量取有限个离散值。本次我们使用两种方法对鸢尾花数据进行聚类。

无监督就是没有标签的进行分类

K-means 聚类算法

K-means聚类算法（k-均值或k-平均）聚类算法。算法思想就是首先随机确定k个中心点作为聚类中心，然后把每个数据点分配给最邻近的中心点，分配完成后形成k个聚类，计算各个聚类的平均中心点，将其作为该聚类新的类中心点，然后迭代上述步骤知道分配过程不在产生变化。

算法流程

随机选择K个随机点（成为聚类中心）
对数据集中的每个数据点，按照距离K个中心点的距离，将其与距离最近的中心点关联起来，与同一中心点关联的所有点聚成一类
计算每一组的均值，将改组所关联的中心点移动到平均值位置
重复上两步，直至中心点不再发生变化

优缺点

优点：

原理比较简单，实现容易，收敛速度快
聚类效果比较优
算法可解释度比较强
主要需要调参的参数仅仅是簇数K

缺点：

K值选取不好把握
不平衡数据集聚类效果不佳
采用迭代方法，得到结果只是局部最优
对噪音和异常点比较敏感

鸢尾花聚类

数据集

数据集：数据集采用sklern中的数据集

数据集分布图：我们可以看出数据的大致分布情况

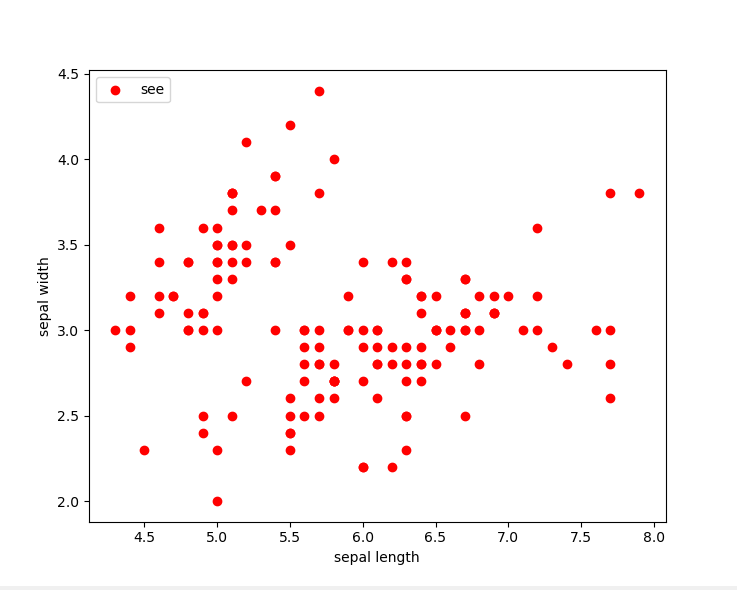
使用sklearn中的模型

# 鸢尾花数据集 150 条数据

## 导包
import numpy as np
import matplotlib.pyplot as plt

# 导入数据集包
from sklearn import datasets

from sklearn.cluster import KMeans

## 加载数据据集
iris = datasets.load_iris()

X = iris.data[:,:4]
print(X.shape)  # 150*4

## 绘制二维数据分布图
## 前两个特征

plt.scatter(X[:,0],X[:,1],c=\'red\',marker=\'o\',label=\'see\')
plt.xlabel(\'sepal length\')
plt.ylabel(\'sepal width\')
plt.legend(loc=2)
plt.show()

\'\'\'
直接调用包
\'\'\'

## 实例化K-means类，并定义训练函数
def Model(n_clusters):
    estimator = KMeans(n_clusters=n_clusters)
    return estimator
## 定义训练韩硕
def train(estimator):
    estimator.fit(X)


## 训练
estimator = Model(3)

## 开启训练拟合
train(estimator=estimator)


## 可视化展示

label_pred = estimator.labels_ # 获取聚类标签

## 找到3中聚类结构
x0 = X[label_pred==0]
x1 = X[label_pred==1]
x2 = X[label_pred==2]

plt.scatter(x0[:,0],x0[:,1],c=\'red\',marker=\'o\',label=\'label0\')
plt.scatter(x1[:,0],x1[:,1],c=\'green\',marker=\'*\',label=\'label1\')
plt.scatter(x2[:,0],x2[:,1],c=\'blue\',marker=\'+\',label=\'label2\')

plt.xlabel(\'sepal length\')
plt.ylabel(\'sepal width\')
plt.legend(loc=2)
plt.show()

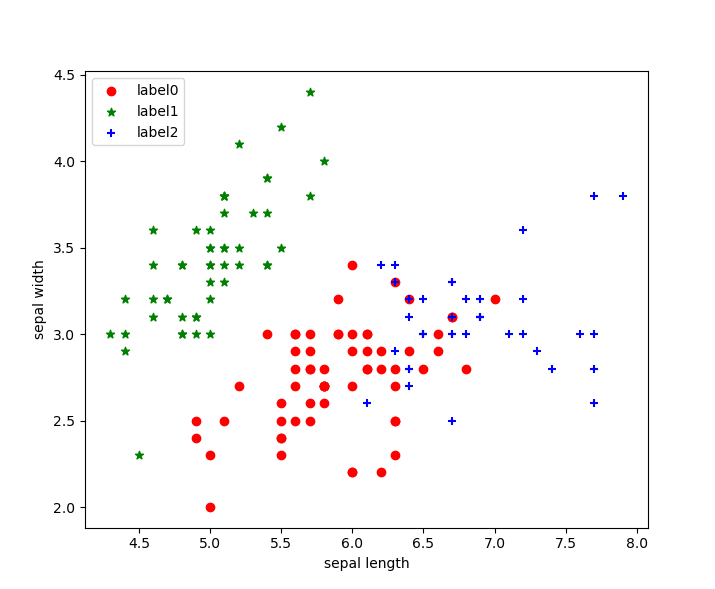
聚类结果

我们可以看出聚类结果按照我们的要求分为了三类，分别使用红、蓝、绿三种颜色进行了展示！
聚类效果图：

手写K-means算法

# 鸢尾花数据集 150 条数据

## 导包
import numpy as np
import matplotlib.pyplot as plt

# 导入数据集包
from sklearn import datasets

from sklearn.cluster import KMeans

## 加载数据据集
iris = datasets.load_iris()

X = iris.data[:,:4]
print(X.shape)  # 150*4

## 绘制二维数据分布图
## 前两个特征

plt.scatter(X[:,0],X[:,1],c=\'red\',marker=\'o\',label=\'see\')
plt.xlabel(\'sepal length\')
plt.ylabel(\'sepal width\')
plt.legend(loc=2)
plt.show()

\'\'\'
直接手写实现
\'\'\'

\'\'\'
1、随机初始化 随机寻找k个簇的中心
2、对这k个中心进行聚类
3、重复1、2，知道中心达到稳定
\'\'\'

### 欧氏距离计算
def distEclud(x,y):
    return np.sqrt(np.sum((x-y)**2))

### 为数据集定义簇的中心
def randCent(dataSet,k):
    m,n = dataSet.shape
    centroids = np.zeros((k,n))
    for i in range(k):
        index = int(np.random.uniform(0,m))
        centroids[i,:] = dataSet[index,:]

    return centroids

## k均值聚类算法
def KMeans(dataSet,k):
    m = np.shape(dataSet)[0]

    clusterAssment = np.mat(np.zeros((m,2)))
    clusterChange = True

    ## 1 初始化质心centroids
    centroids = randCent(dataSet,k)

    while clusterChange:
        # 样本所属簇不在更新时停止迭代
        clusterChange = False

        # 遍历所有样本
        for i in range(m):
            minDist = 100000.0
            minIndex = -1

            # 遍历所有质心
            # 2 找出最近质心
            for j in range(k):
                distance = distEclud(centroids[j,:],dataSet[i,:])
                if distance<minDist:
                    minDist = distance
                    minIndex = j

            # 更新该行所属的簇
            if clusterAssment[i,0] != minIndex:
                clusterChange = True
                clusterAssment[i,:] = minIndex,minDist**2

        # 更新质心
        for j in range(k):
            pointsInCluster = dataSet[np.nonzero(clusterAssment[:,0].A == j)[0]] # 获取对应簇类所有的点
            centroids[j,:] = np.mean(pointsInCluster,axis=0)

    print(\"cluster complete\")
    return centroids,clusterAssment


def draw(data, center, assment):
    length = len(center)
    fig = plt.figure
    data1 = data[np.nonzero(assment[:,0].A == 0)[0]]
    data2 = data[np.nonzero(assment[:,0].A == 1)[0]]
    data3 = data[np.nonzero(assment[:,0].A == 2)[0]]

    # 选取前两个数据绘制原始数据的散点

    plt.scatter(data1[:,0],data1[:,1],c=\'red\',marker=\'o\',label=\'label0\')
    plt.scatter(data2[:,0],data2[:,1],c=\'green\',marker=\'*\',label=\'label1\')
    plt.scatter(data3[:,0],data3[:,1],c=\'blue\',marker=\'+\',label=\'label2\')

    # 绘制簇的质心点
    for i in range(length):
        plt.annotate(\'center\',xy=(center[i,0],center[i,1]),xytext=(center[i,0]+1,center[i,1]+1),arrowprops=dict(facecolor=\'yellow\'))

    plt.show()

    # 选取后两个维度绘制原始数据散点图
    plt.scatter(data1[:, 2], data1[:, 3], c=\'red\', marker=\'o\', label=\'label0\')
    plt.scatter(data2[:, 2], data2[:, 3], c=\'green\', marker=\'*\', label=\'label1\')
    plt.scatter(data3[:, 2], data3[:, 3], c=\'blue\', marker=\'+\', label=\'label2\')

    # 绘制簇的质心点
    for i in range(length):
        plt.annotate(\'center\', xy=(center[i, 2], center[i, 3]), xytext=(center[i, 2] + 1, center[i, 3] + 1),
                     arrowprops=dict(facecolor=\'yellow\'))

    plt.show()


## 调用

dataSet = X
k = 3
centroids,clusterAssment = KMeans(dataSet,k)
draw(dataSet,centroids,clusterAssment)

效果图展示

我们可以看到手写实现的也通过三种颜色实现类，可以看出两种方式实现结果是几乎相同的。

根据花萼长度花萼宽度聚类
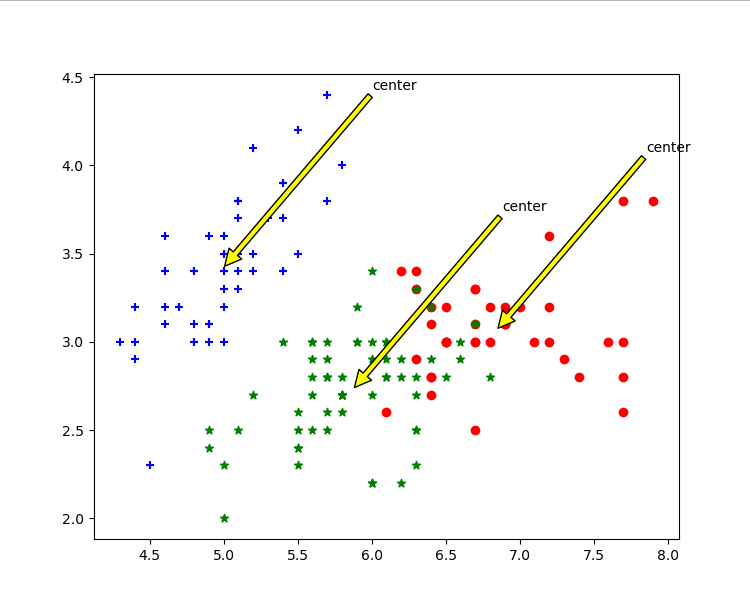
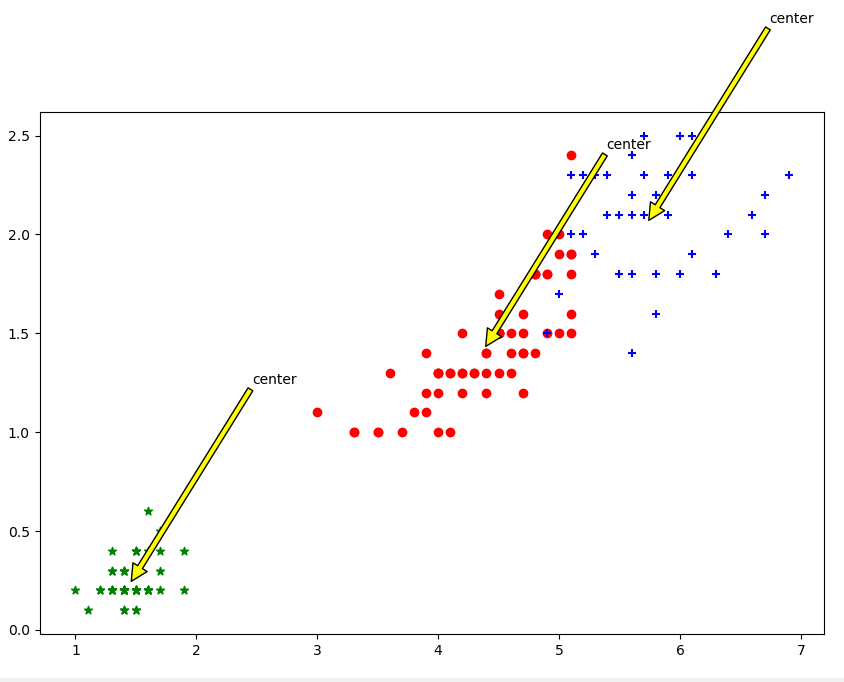
根据花瓣长度花瓣宽度聚类：

总结

我们既可以使用sklearn包中封装好的模型进行聚类分析，也可以自己手写实现，在某些问题上，两者都可以达到相同的结果，我们对于不同的问题可以更合适的方法进行处理。

来源：https://www.cnblogs.com/hjk-airl/p/16410359.html
本站部分图文来源于网络，如有侵权请联系删除。

【机器学习】K-means聚类分析

前言