百木园本章绘图要点:
- 生成元算法：重复性的绘图步骤可抽象提炼成数据，保存在列表或元组里，然后，依据抽象规则，读取数据，调用绘图函数，生成所需要的图形，从而降低程序的复杂性，减少程序的代码量。
- 绘图效率：当图形的数据计算量比较大时，可先统一计算，然后再绘图，从而提高图形的生成效率。
一生二，二生三
“道生一，一生二，二生三，三生万物。
--《道德经》
为什么相对少量的遗传物质可以发育成复杂的结构，如肺、大脑、心脏？
为什么只占人体体积5％的血管能遍布人体的每一部分？
生命究竟是什么？生命最初又是如何形成的？
基因存在于染色体上，负责对生命体的形态、结构、功能进行全方位的编码，它所包含的信息必定有限，然而如此有限的信息又是如何准确地描述后代生命的性状？
经典理论无法解释自然界这些让人困惑的问题，直到分形理论的出现，才让这些问题有了一个可能的答案。简单而少量的规则是可以生成复杂结构的，自然界中的许多事物可以通过简单步骤的无数次重复（也就是分形迭代）演化而成。
由一个简单的生成因子（分形理论中称之为“生成元”），不断迭代，自我进化，越来越复杂，以至于逐步出现山川、草木、动物、人类及人类的思维。宇宙间的一切难道都是这样动态生成的吗？听起来不可思议，但或许这就是事实！
生成元
我们可以在计算机上做个小实验，用『原形+生成元+迭代』的方式，来生成一些复杂的图形。上一章的科赫曲线的原形是一条直线，生成元是：
如果保持原形为一条直线，改变生成元，那么多次迭代后，会生成一个怎么样的图形呢？
生成元1：
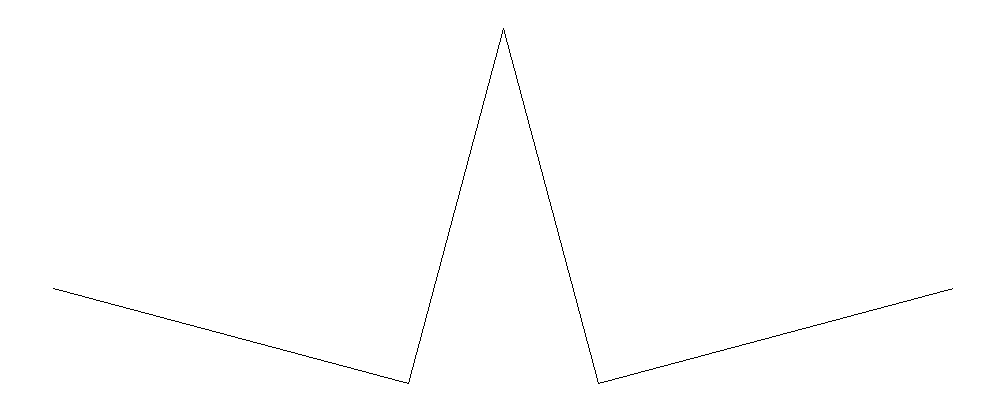
第一次迭代同生成元；
第二次迭代：
第三次迭代：
第六次迭代：
生成元2：
第一次迭代同生成元；
第二次迭代：
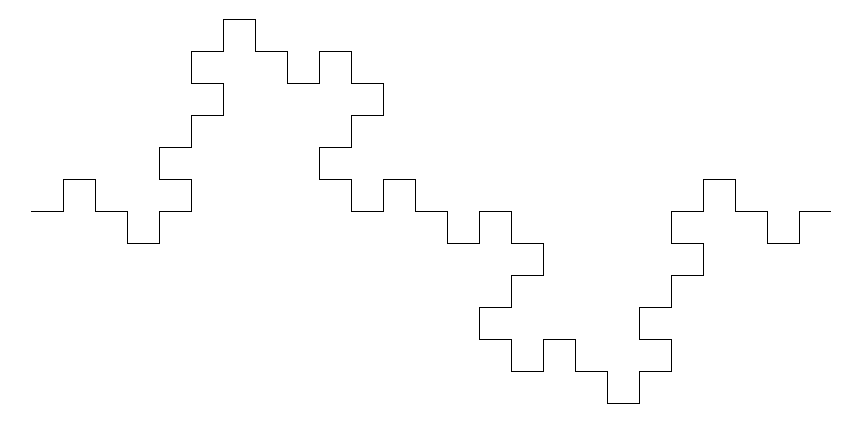
第三次迭代：
第四次迭代：
你可以尝试设计不同的生成元，多次迭代后，看看会生成怎样复杂的图形。为了更清晰地显示图形的细微结构，示例程序画笔的颜色选择的是默认的黑色，你也可以选择自己喜欢的单种或多种颜色，来生成更绚烂的图形。
2.3 算法
我们可以用一个列表genu来指定生成元，例如科赫曲线的生成元可用列表gene = [0,60,-120,60,END]来表示：
列表的每个值表示了旋转角的大小，正数是逆时针旋转，负数是顺时针旋转。A点不旋转，为0；C点逆时针旋转60度，为60；D点顺时针旋转120，为-120；E点逆时针旋转60，为60；END表示终止指定生成元(实际上它可以是任意值)。从一次旋转到下次旋转之间的距离是一定的，也就是说，AC、CD、DE、EB的长度是相同的，都为AB的1/3。
除了生成元以外，我们还需要一个缩小率ratio：下一次迭代的线段和原始线段的比率，也就是AC/AB，科赫曲线的这个比率我们知道就是1/3，约为0.3333。
生成元1 的生成元可用列表[-15,90,-150,90,END]来表示：
列表的每个值表示了旋转角的大小，正数是逆时针旋转，负数是顺时针旋转。A点顺时针旋转15，为-15；C点逆时针旋转90度，为90；D点顺时针旋转150，为-150；E点逆时针旋转90，为90；END表示终止指定生成元。 AC、CD、DE、EB的长度是相同的。
生成元1 的缩小率ratio（下一次迭代的线段和原始线段的比率），也就是AC/AB，这个比率我们通过计算可知：
ratio =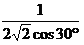
= 0.40824829046386296 ≈ 0.4082
生成元2 的生成元可用列表[0,90,-90,-90,90,-90,90,90,-90,END]来表示：
列表的每个值表示了旋转角的大小，正数是逆时针旋转，负数是顺时针旋转。生成元2 的缩小率为:
ratio = 1/5 = 0.2
下表为几种曲线的生成元和缩小率：
|
|
科赫曲线 |
生成元1 |
生成元2 |
|
生成元gene |
[0,60,-120,60,END] |
[-15,90,-150,90,END] |
[0,90,-90,-90,90,-90,90,90,-90,END] |
|
缩小率ratio |
1/3 ≈ 0.3333 |
0.4082 |
1/5 = 0.2 |
源码
# 导入模块
import turtle
# 恢复海龟状态到p点
def restore(p):
turtle.penup()
turtle.setpos(p[0],p[1])
turtle.pendown()
turtle.seth(p[2])
# 获取海龟当前点状态
def get_point():
x,y = turtle.pos()
d = turtle.heading()
return (x,y,d)
# 生成器函数，A为起始点，B为结束点，L为线段AB的长度，genu为生成元，ratio为缩小率，n为迭代次数
def Generator(A,B,L,genu,ratio,n):
# 获取图形各个点的位置和方向，不显示图形
restore(A)
turtle.pencolor(b_color) # 画笔颜色设置和背景色相同，不显示图形
points = []
for angle in gene:
if angle == \'END\':
break
else:
angle = int(angle)
if angle < 0:
turtle.right(abs(angle))
else:
turtle.left(angle)
p = get_point()
points.append(p)
turtle.forward(L*ratio)
points.append(B)
turtle.pencolor(p_color) # 恢复画笔颜色
if n == 1:
# 绘制图形
restore(A)
for p in points:
turtle.setpos(p[0],p[1])
else:
# 递归调用生成器，使用生成元替换中间线段
i = 0
while i <len(points)-1:
Generator(points[i],points[i+1],L*ratio,gene,ratio,n-1)
i = i+1
# 开始主程序
if __name__ == \'__main__\':
# 隐藏画笔形状
turtle.hideturtle()
# 指定画笔的速度，参数speed为0到10之间的一个整数，1最慢，10最快
turtle.speed(9)
# 指定画笔大小
turtle.pensize(1)
# 设置颜色模式为RGB
turtle.colormode(255)
# 背景颜色为青色,画笔颜色为白色
b_color = (136,168,155)
p_color = \'white\'
# 设置背景颜色
turtle.bgcolor(b_color)
# 原形为一条直线
A = (-450,0,0)
B = (450,0,0)
L = 900
# 获取用户输入的生成元、缩小率、迭代次数
print(\'生成元：\')
gene = input().split(\',\')
print(\'缩小率：\')
ratio = float(input())
print(\'迭代次数：\')
n = int(input())
# 生成图形
restore(A)
Generator(A,B,L,gene,ratio,n)
来源：https://www.cnblogs.com/timedot/p/14547485.html
图文来源于网络，如有侵权请联系删除。