前言
算法是什么?算法就是数学规律.怎么去总结和发现这个规律,就是理解算法的过程.
KMP算法的本质是穷举法,而并不是去创造新的匹配逻辑.
以下将搜寻的字符串称为子串(part),以P表示.被搜寻的字符串称为总串(total),以T表示.
start代表P串在T串中开始匹配的位置,end代表P串与T串对比字符时的位置
String total = \"ababcd\";
String part = \"abc\";
total.contains(part);
部分匹配表
部分匹配表是KMP算法的核心。只要理解了部分匹配表,就基本理解了KMP算法。
普通匹配模式
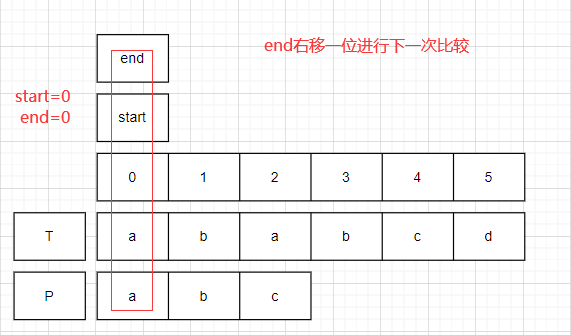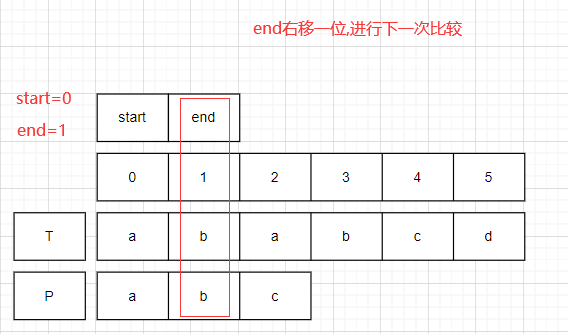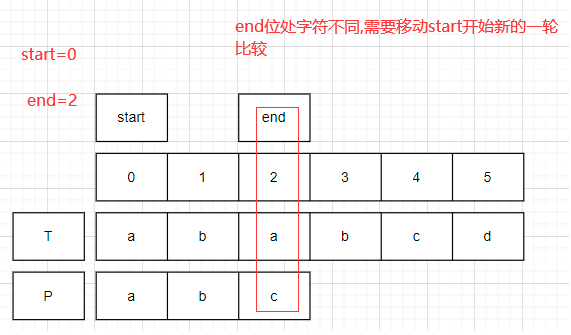
对比开始.
start=0,end=0;比较T.charAt(0)==P.charAt(0).均为a,此时end右移一位.
start=0,end=1;比较T.charAt(1)==P.charAt(1).均为b,此时end右移一位.
start=0,end=2;比较T.charAt(2)!=P.charAt(2).此时,start右移一位.
start=1,end=0;比较T.charAt(start+end)!=P.charAt(end).此时,start右移一位.
start=2,end=0;比较T.charAt(start+end)==P.charAt(end).此时,此时end右移一位.以此类推.
最终发现T.contains(P)为true,T.indexOf(P)为start,即为2.
public static int getIndex(String total, String part) {
char[] totalChars = total.toCharArray();
char[] partChars = part.toCharArray();
int start = 0;
int end = 0;
while (start < total.length()) {
if (totalChars[start + end] == partChars[end]) {
end++;
} else {
start = start + 1;
end = 0;
}
if (end == part.length()) {
return start;
}
}
return -1;
}
寻找规律
规律是什么?就是在匹配过程中,遇到某一位不匹配时.start与end下一次的起点位置选择.
对于普通匹配而言,start的变化永远是右移一位,end永远是从0开始,并且每次右移一位.
这里先介绍两个规律,当发现end位不匹配时
第一条规律,,新起点位置只与重合部分有关
T.charAt(start+end)!=P.charAt(end)
T.substring(start,start+end)==P.substring(0,end)
因为它不相等,所以它相等,这句话前后顺序不能颠倒.这虽然很像废话,但是确实KMP算法的核心.
第二条规律,未知无法跳过
这次的end位一定是下次比较的起点
这里有个特殊的地方,就是首位不同时的逻辑,代码中也是一样,先按下不表.
部分匹配表
有个比较关键的地方,确定start与end新起点的规则是什么?
新的起点是什么,是可能性,是T串的某一段与P串完全相同的可能性.
只有end=0时相同,才会有end=1时的比较
只有end=1时相同,才会有end=2时的比较
...
那么至少,T.charAt(start)==P.charAt(0),才可以进行后面的比较
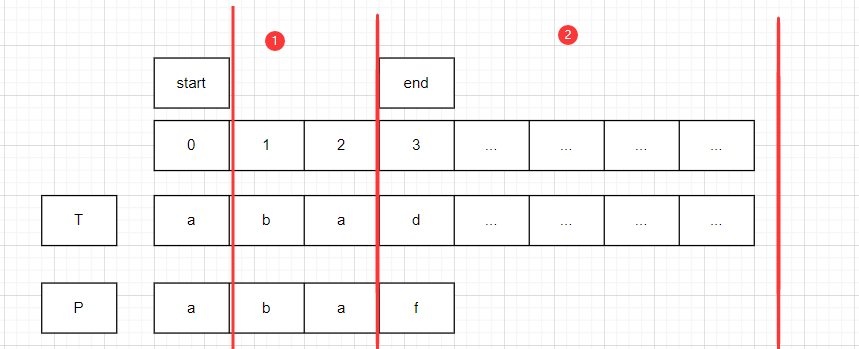
当遇到end位不匹配时,我们将start可能移动的轨迹分为两部分
① (start,start+end)
② [start+end,...]
T.indexOf(P)的位置只可能出现在这两个区域(因为之前的位置都被排除了).这两个区域的差别是什么呢?
结合上面两条规律,途经区域①的比较的字符对象是完全已知的,而区域②则不是.
即下一次start的起点在 (start,start+end] 中
因为即要么在(start,start+end)中,要么就是end,因为end是未知的,必须要用首位去对比,所以start最远会位移到end位
由于第一条规律,T.substring(start,start+end)==P.substring(0,end)
那么start在T.substring(start,start+end)中位移的过程就是start在P.substring(0,end)中位移的过程
去寻找start在(start,start+end)中作为新起点的可能性,就是寻P.substring(0,end)这个字符串本身与其子串的重合度,什么是重合度?
两个相同的字符串,一个不动,一个整体向右移动一格,查看两者相交部分,如果相交部分完全相等,那么相交字符串的首位,就是新的起点,这个相交部分的长度就是重合度.
假设 P = abcde
| 不匹配时end位置 | P.substring(0,end) | 重合度 |
|---|---|---|
| 0 | \"\" | 0 |
| 1 | a | 0 |
| 2 | ab | 0 |
| 3 | abc | 0 |
| 4 | abcd | 0 |
获取重合度
public static int getPublicPart(String part) {
int start = 1;
int end = 0;
char[] chars = part.toCharArray();
while (start < part.length()) {
if (chars[start + end] == chars[end]) {
if (end + start == part.length() - 1) {
return part.substring(start).length();
}
end++;
} else {
start++;
end = 0;
}
}
return 0;
}
我们将start移动轨迹的研究,变成了P.substring(0,end)的研究,那么假设T串很长,那么end值可能会出现在任意一个地方,并且相同情况会有多次,所以我们只要事先将所有可能的情况列出,以后遇到相同情况就可以直接套用结果.
为什么可以复用呢?因为P.charAt(end)我们一定知道什么,但是T.charAt(start+end)却有很多种可能,因为它只需要与P.charAt(end)不相等
假设 P = aaaab
| 不匹配时end位置 | P.substring(0,end) | 重合度 | 下一次start位置 | 下一次end位置 |
|---|---|---|---|---|
| 4 | aaaa | 3 | start+4-3 | 3 |
| 3 | aaa | 2 | start+3-2 | 2 |
| 2 | aa | 1 | start+2-1 | 1 |
| 1 | a | 0 | start+1-0 | 0 |
| 0 | \"\" | 0 | start+0-(-1) | 0 |
我们可以发现,start下一次的位置为 start +( end - P.substring(0,end)的重合度). (end - 重合度) 其实就是start需要位移的距离
end下一次的位置为 P.substring(0,end)的重合度
但是由于P.substring(0,0)为空字符串,比较特殊,首位不同时,start是直接右移一位
故令next[0] = -1 , 当 next[end] < 0时,下一次的end位置指向 0
获取next数组
public static int[] getNext(String part) {
int[] next = new int[part.length()];
int start = 1;
while (start < part.length()) {
next[start] = getPublicPart(part.substring(0, start));
start++;
}
next[0] = -1;
return next;
}
我们将end位不同时,P.substring(0,end)它的子串与自身的重合度,称之为部分匹配表
Tips:
这里有一个很关键的地方,start可以直接从0移动到2吗?不可以,因为KMP无法违背普通匹配,或者说违背匹配的规律,只有start每次右移一位,即P.charAt(0)与T串的每一位开始比较,才能确认这个位置含不含有可能性,而我们next数组的获取就是通过每次右移一位获取到的.
完整代码
KMP算法的本质就是通过穷举end位不匹配时start与end的移动轨迹,来达到复用的效果.
public static int indexOf(String total, String part) {
char[] totalChars = total.toCharArray();
char[] partChars = part.toCharArray();
int[] next = getNext(part);
int start = 0;
int end = 0;
while (start < total.length()) {
if (totalChars[start + end] == partChars[end]) {
end++;
} else {
// 与普通匹配不同的其实就是end位不同时,下一次start与end的位置选择
start = start + end - next[end];
end = Math.max(0, next[end]);
}
if (end == part.length()) {
return start;
}
}
return -1;
}
小小的一篇文章,写了快一个月,每天晚上将思想转化为文字时,总会有新的理解,修修改改了这么长时间,总觉得文字不够干练.人生亦是如此.
本文来自博客园,作者:狸子橘花茶,转载请注明原文链接:https://www.cnblogs.com/yusishi/p/16403675.html
来源:https://www.cnblogs.com/yusishi/p/16403675.html
本站部分图文来源于网络,如有侵权请联系删除。
 百木园
百木园