Python数据分析--Numpy常用函数介绍(9)-- 与线性代数有关的模块linalg

numpy.linalg 模块包含线性代数的函数。使用这个模块，可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等。
一、计算逆矩阵

线性代数中，矩阵A与其逆矩阵A ^(-1)相乘后会得到一个单位矩阵I。该定义可以写为A *A ^(-1) =1。numpy.linalg 模块中的 inv 函数可以计算逆矩阵。

1) 用 mat 函数创建示例矩阵

import numpy as np
import matplotlib.pyplot as plt

A = np.mat(\"0 1 2;1 0 3;4 -3 8\")

2)用 inv 函数计算逆矩阵

inverse = np.linalg.inv(A)
print(\"inverse of A\\n\", inverse)

运行结果如下：

A
 [[ 0  1  2]
 [ 1  0  3]
 [ 4 -3  8]]
inverse of A
 [[-4.5  7.  -1.5]
 [-2.   4.  -1. ]
 [ 1.5 -2.   0.5]]

 3）可能通过原矩阵和逆矩阵相乘的结果来验证

print (\"Check\\n\", A * inverse) #验证计算，原矩阵和逆矩阵相乘的，单位矩阵

结果：

Check
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

二、求解线性方程组

线性议程组  Ax=b

1)分另创建矩阵A和数组b

A = np.mat(\"1 -2 1;0 2 -8;-4 5 9\") #用mat()函数创建示例矩阵
print(\"A\\n\", A)
b = np.array([0, 8, -9])

2)用solve(A, b)解出x，用dot()函数进行验证，并打印

x = np.linalg.solve(A, b)
print(\"Solution\", x)
print(\"Check\\n\", np.dot(A , x)) #用dot()函数检查求得的解是否正确

三、特征值和特征向量

特征值（eigenvalue）即方程 Ax = ax 的根，是一个标量，特征向量是关于特征值的向量。在numpy.linalg 模块中， eigvals函数可以计算矩阵的特征值，而 eig 函数可以返回一个包含特征值和对应的特征向量的元组。

用 eigvals 函数求解特征值

用 eig 函数求解特征值和特征向量 ,如下代码：

print(\"Eigenvalues\", np.linalg.eigvals(A))
eigenvalues, eigenvectors = np.linalg.eig(A)
print( \"First tuple of eig\", eigenvalues)
print(\" Second tuple of eig\\n\", eigenvectors)

四、奇异值分解

奇异值分解，是一种因子分解运算，将一个矩阵分解为3个矩阵的乘积。奇异值分解是特征值分解一种推广。在 numpy.linalg 模块中的svd()函数可以对矩阵进行奇异值分解。该函数返回3个矩阵——U、Sigma和V，其中U和V是正交矩阵，Sigma包含输入矩阵的奇异值（计算出来结果可能是虚数）。

U, Sigma, V = np.linalg.svd(A, full_matrices=False)# 用svd() 函数分解矩阵
print (\"U:\",U)
print (\"Sigma:\",Sigma)
print (\"V:\", V)
print (\"Product\\n\", U * np.diag(Sigma) * V) #用diag函数生成完整的奇异值矩阵

 五、广义

pinv 函数进行求解，计算广义逆矩阵需要用到奇异值分解函数pinv()，行列式计算用np.linalg中的函数det()： 

#使用pinv函数计算广义逆矩阵:
A = np.mat(\"4 11 14;8 7 -2\")
pseudoinv = np.linalg.pinv(A)
print(\"Pseudo inverse:\\n\", pseudoinv)
#计算矩阵的行列式
print(\"\\n\")
B = np.mat(\"3 4;5 6\")
print(\"Determinant:\", np.linalg.det(B))

全部代码如下：

import numpy as np
import matplotlib.pyplot as plt

A = np.mat(\"0 1 2;1 0 3;4 -3 8\")  #用mat()函数创建示例矩阵
print (\"A\\n\",A)
inverse = np.linalg.inv(A)  #用inv()函数计算逆矩阵
print(\"inverse of A\\n\", inverse)
print (\"Check\\n\", A * inverse) #验证计算，原矩阵和逆矩阵相乘的，单位矩阵
#  求解线性方程组
A = np.mat(\"1 -2 1;0 2 -8;-4 5 9\") #用mat()函数创建示例矩阵
b = np.array([0, 8, -9])
x = np.linalg.solve(A, b)
print(\"Solution\", x)
print(\"Check\\n\", np.dot(A , x))  #用dot()函数检查求得的解是否正确
#特征值和特征向量

print(\"Eigenvalues\", np.linalg.eigvals(A))   #eigvals函数可以计算矩阵的特征值
eigenvalues, eigenvectors = np.linalg.eig(A) #用 eig 函数求解特征值和特征向量
print( \"First tuple of eig\", eigenvalues)
print(\" Second tuple of eig\\n\", eigenvectors)

#奇异值分解
U, Sigma, V = np.linalg.svd(A, full_matrices=False)# 用svd() 函数分解矩阵
print (\"U:\",U)
print (\"Sigma:\",Sigma)
print (\"V:\", V)
print (\"Product\\n\", U * np.diag(Sigma) * V) #用diag函数生成完整的奇异值矩阵
#使用pinv函数计算广义逆矩阵:
A = np.mat(\"4 11 14;8 7 -2\")
pseudoinv = np.linalg.pinv(A)
print(\"Pseudo inverse:\\n\", pseudoinv)
#计算矩阵的行列式
print(\"\\n\")
B = np.mat(\"3 4;5 6\")
print(\"Determinant:\", np.linalg.det(B))

运行结果：

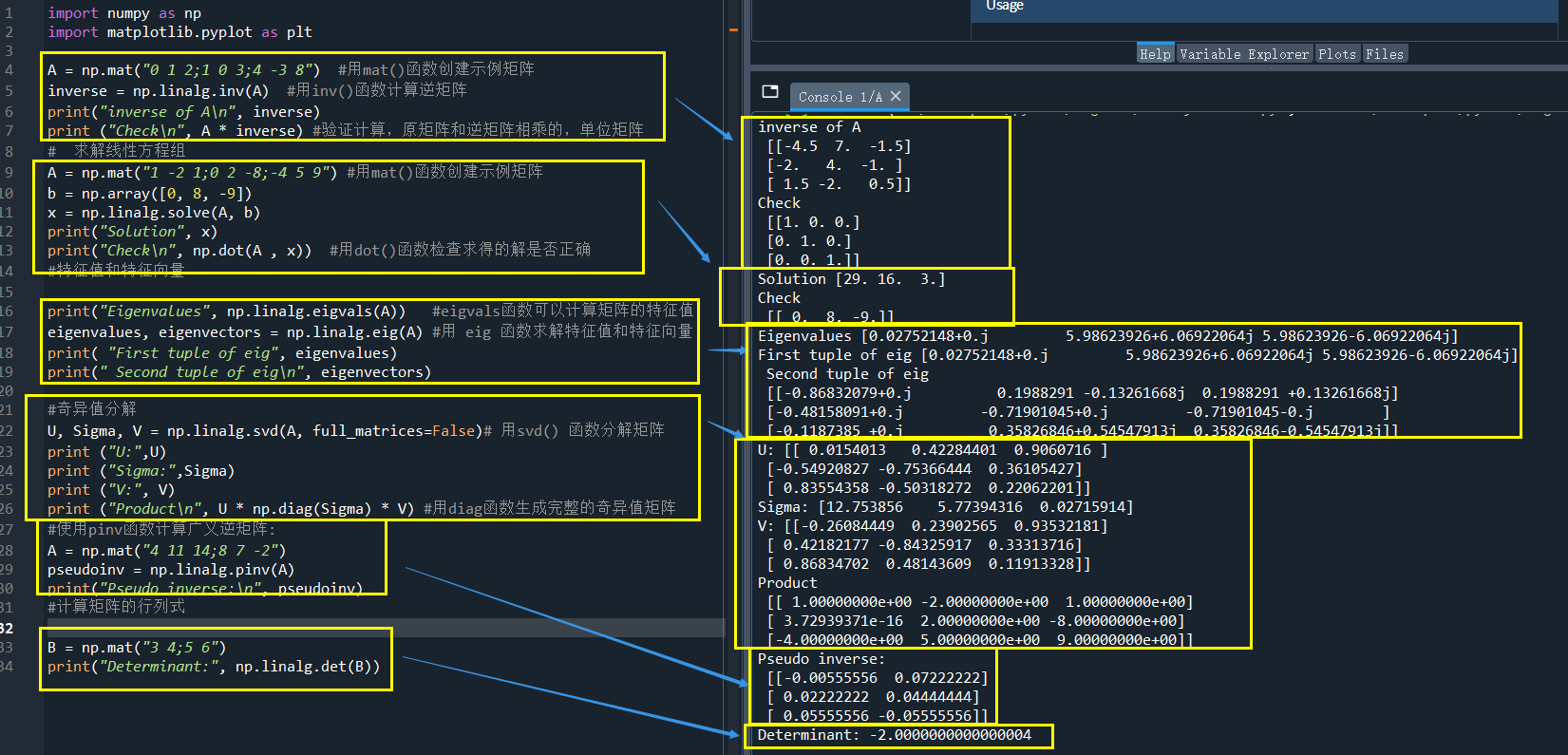
本篇介绍了一些numpy.linalg 模块中常用的函数，

来源：https://www.cnblogs.com/codingchen/p/16364993.html
本站部分图文来源于网络，如有侵权请联系删除。