
决策树模型是监督学习算法中比较经典的模型,作为策略产品经理必须要了解该模型。本篇将通俗易懂地给大家讲解树模型的基本概念,树模型的种类,如何去选取决策节点,如何剪枝等。
一、什么是决策树
1. 基本概念
决策树(Decision Tree)是监督学习算法的一种,主要应用于分类问题,但有时也会应用在回归问题上。从数据中挑选具有区分性的变量,将数据集拆分为两个或两个以上的子集合,一步一步拆分,最终形成了一棵“树”,“树”的每个叶子节点代表该分支最终的预测结果。
我们通过几组示例形象地展现什么是决策树模型。下图是2020年美国大选10位选民的个人信息,一共有四个特征:年龄、性别、年收入和肤色,四个特征为输入变量。最后一列是各自最终投票的总统候选人,为目标变量。
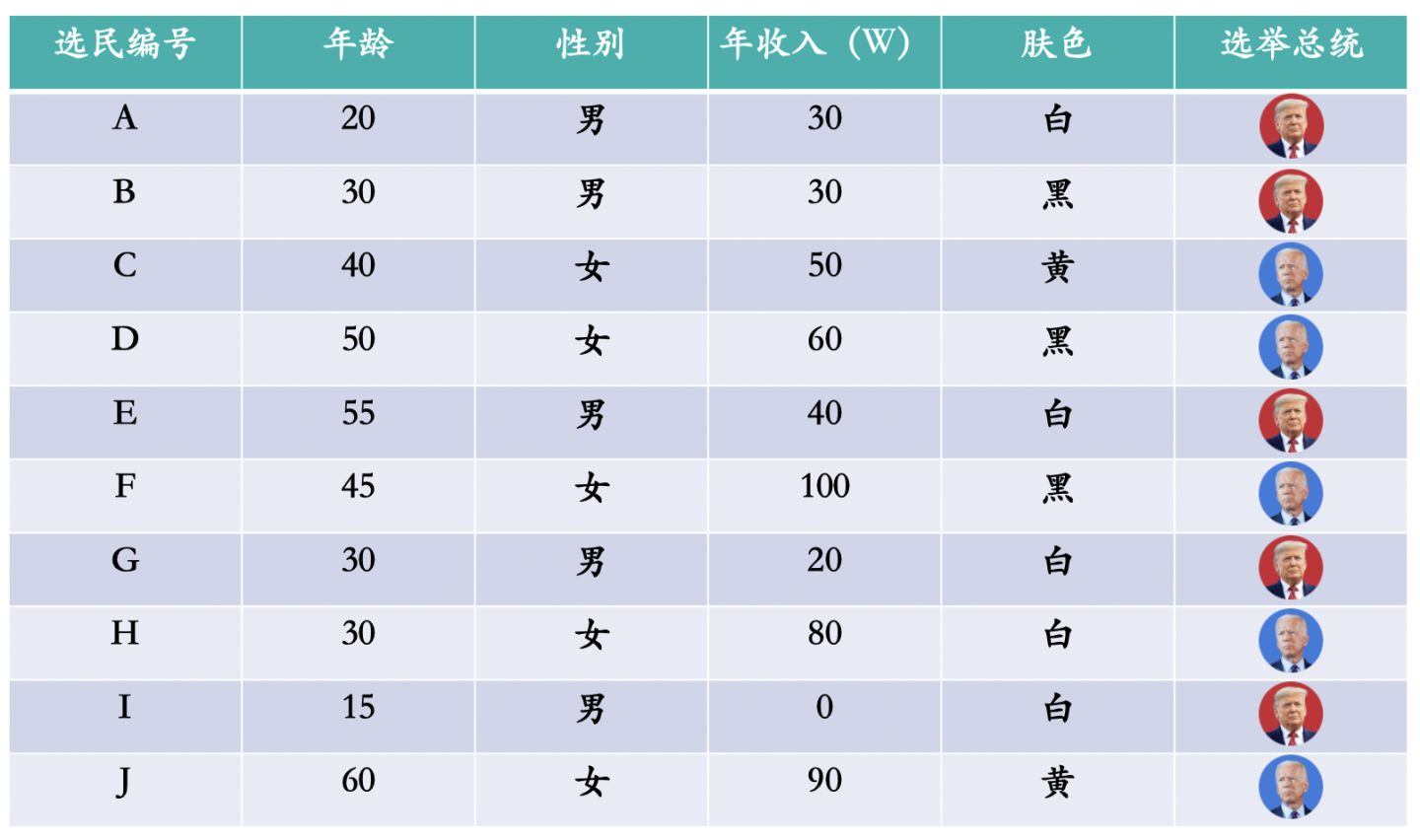
我们以年龄、性别、年收入和肤色四个特征,分别构建四组决策树模型,如下图:
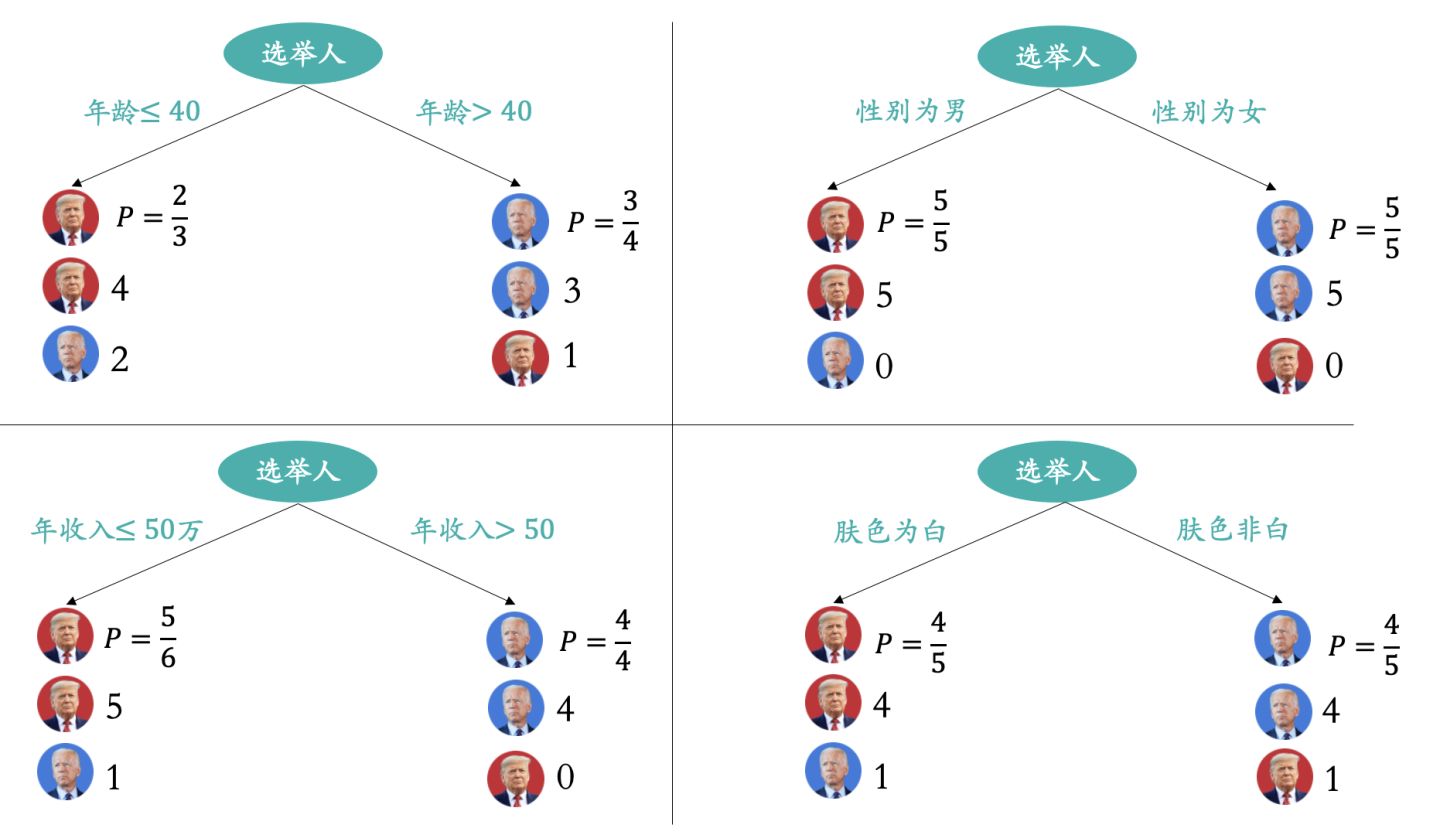
通过上图,我们可以看出选择性别这个特征构建的决策树模型效果是最好的,树模型里面的分支是“选民性别为男时会投票给川建国”,“选民性别为女时会投票给拜振华”。根据数据集显示,该决策树预测的准确率为100%,这就是一个简单的决策树模型。当然我们也可以将多个特征融合在一起构建成一个决策树如下图。

介绍完上述决策树模型如何运作的,下图是决策树模型中的一些专业术语:根节点、叶子节点、决策节点、拆分、剪枝、父节点&孩子节点。
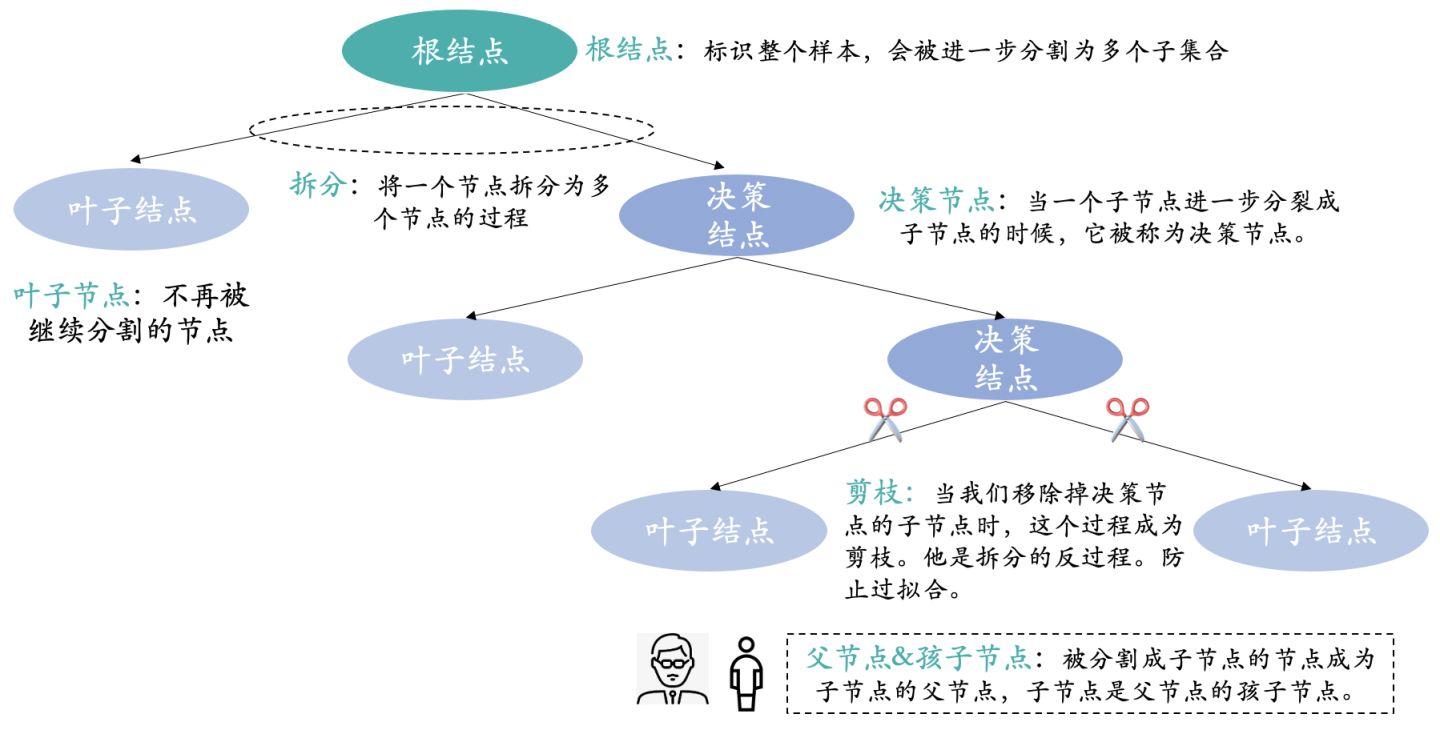
2. 决策树模型分类

决策树模型从大的分类来讲,分为“分类树”和“回归树”。当我们最终预测的目标变量是一个离散值时,我们使用“分类树”。当我们最终预测的目标变量是一个连续值时,我们使用“回归树”。
1)分类树
当一条新的测试数据进入到分类树的某个子节点时,分类树模型会使用该子节点内所有训练数据的目标变量的众数作为新数据的预测值。
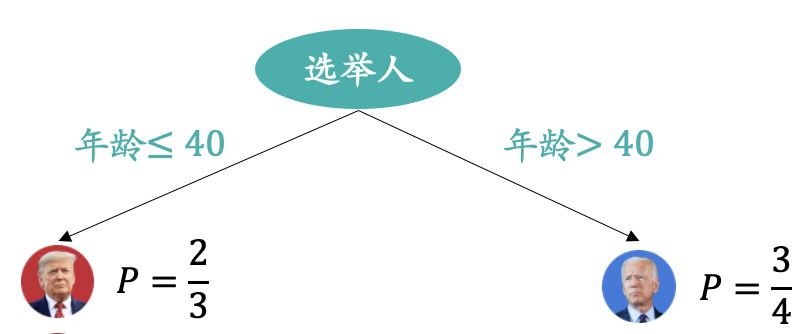
比如某位选民,他的年龄为28岁,我们预测他最终会投票给谁。在上述决策树模型中就会被归类到左侧子节点,而左侧子节点中大部分都是投票给川建国,所以模型预测的结果是投票给川建国。
2)回归树
当一条新的测试数据进入到回归树的某个子节点时,回归树模型会使用该子节点内所有训练数据的目标变量的平均数作为新数据的预测值。
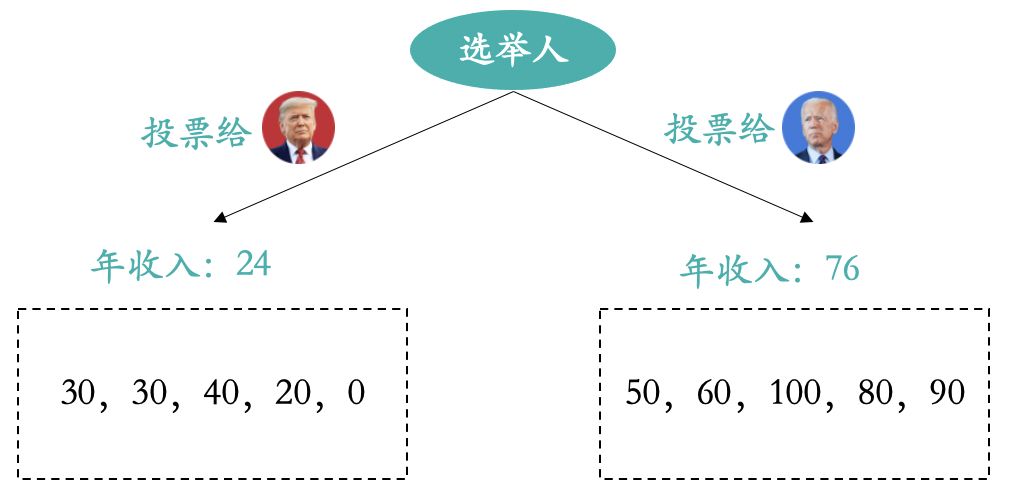
本次案例中我们以选民的年收入为目标变量,选举的总统为输入变量。
比如某位选民将票投给了拜振华,现在预测该选民的年收入。那么在上述回归树模型中就会被归类到右侧子节点,模型预测他的年收入就是所有样本的平均值,也就是76W。
二、树模型的拆分
上述拜振华和川建国的选民特征一共只有四个,且每个特征内的值都很少。我们可以快速地看出选择哪个特征来构建树模型效果更好。但实际场景中,数据的特征会很多,同时每个特征的值也会非常多。那么我们选择哪些特征或者特征组合来构建树模型?针对单个特征又在具体哪个值进行拆分了?拆分的好与坏,通过什么指标来衡量了?下面就一一介绍相关方法和评估指标。
1. 基尼不纯度-Gini Impurity
首先和大家解释一下基尼系数(Gini Coefficient)和基尼不纯度(Gini Impurity)的差异。有很多文章在介绍树模型的时候把基尼系数和基尼不纯度混淆在了一起。
1)基尼系数(Gini Coefficient)
基尼系数是用来衡量国家民众之间收入水平差异和贫富情况的,在1912年由意大利科学家 Gini提出。基尼系数越靠近1,说明国家民众之间收入水平差异越大;越靠近0,说明国家民众之间收入水平差异越小。
2)基尼不纯度(Gini Impurity)
我们在评估树模型的分支效果时一般用的指标叫做基尼不纯度,而不叫基尼系数。
基尼不纯度:描述系统的“纯”度,从数据集中随机选择一个子项,衡量其被错误地分类到其他类别的概率。
计算公式:

P_i代表当前节点中属于i类的比例;G(P)∈[0,1],越靠近0越“纯”,分类效果越好。
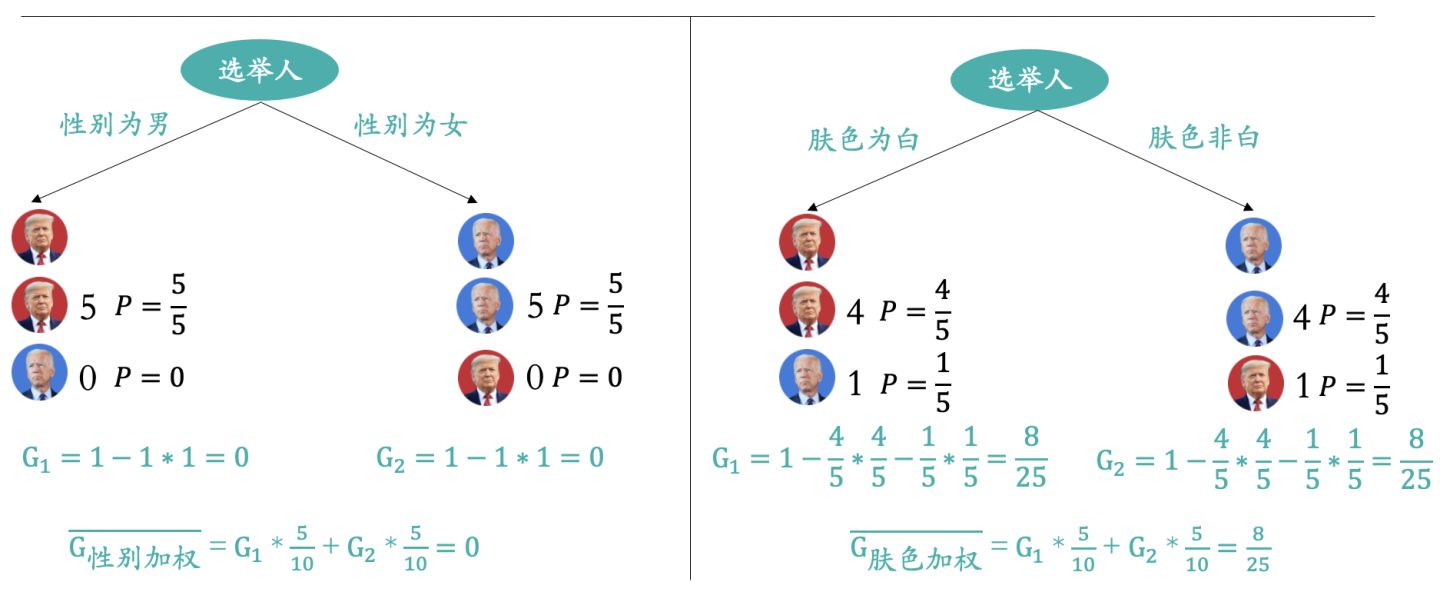
我们仍然以选举的总统作为树模型的预测目标值,首先以性别作为决策节点,经过上图的计算最终的加权基尼不纯度为0;我们再以肤色是否为白作为决策节点,经过上图的计算最终的加权基尼不纯度为8/25,而基尼不纯度越接近于0分类效果越好,所以选择性别作为决策节点更好。
2. 信息增益-Information Gain
除了上述的基尼不纯度,我们还可以用“信息增益”来评估决策节点的分裂效果好坏,信息增益值越大说明分裂效果越好。信息增益的意义在于系统的不确定性减少了多少。在介绍信息增益之前,我们先介绍“熵”。
什么是熵?熵本身是一个热力学的概念,最早我们是在学习物理时接触到的,形容分子运动的混乱程度。在树模型中,我们用熵来衡量信息的不确定性,如果树模型的单个叶子节点信息含有的分类越多,则熵越大。熵越大,表示分裂效果越差。最优的情况就是单个叶子节点只包含一种分类。
计算公式:
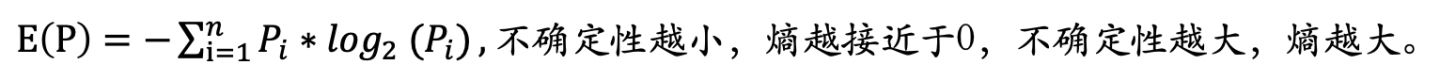
整体步骤如下:

还是选择“性别”和“肤色是否为白”作为决策节点进行相关熵值的计算,左侧的子节点的加权熵为0,右侧的子节点加权熵为0.72,二者的父节点熵均为:
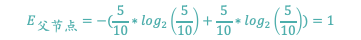
- 选择“性别”作为决策节点,信息增益值:1-0 = 1,即系统的不确定性减少了1
- 选择“肤色是否为白”作为决策节点,信息增益值:1-0.72 = 0.28,即系统的不确定性减少了0.28
所以选择“性别”作为决策节点更好。
1和2介绍的方法适用于分类树,因为我们可以明确样本的分类,计算出P的值,但是在回归树里面是具体的数值,不存在分类,那么回归树的分裂点如何选择,我们使用3的方法。
3. 方差法
该方法简单易懂,通过计算每个叶子节点的方差,然后将所有的方差进行加权,最后选择方差值最小的分裂方法。计算公式如下:
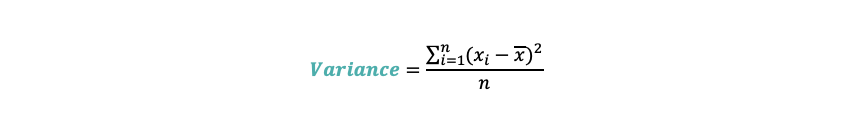
本次样例中,我们将“选民的年收入”作为目标变量,“选民选择的总统“和”选民的肤色“作为输入变量。

如上图,“选民选择的总统”作为输入变量,最终计算出的加权方差为264;
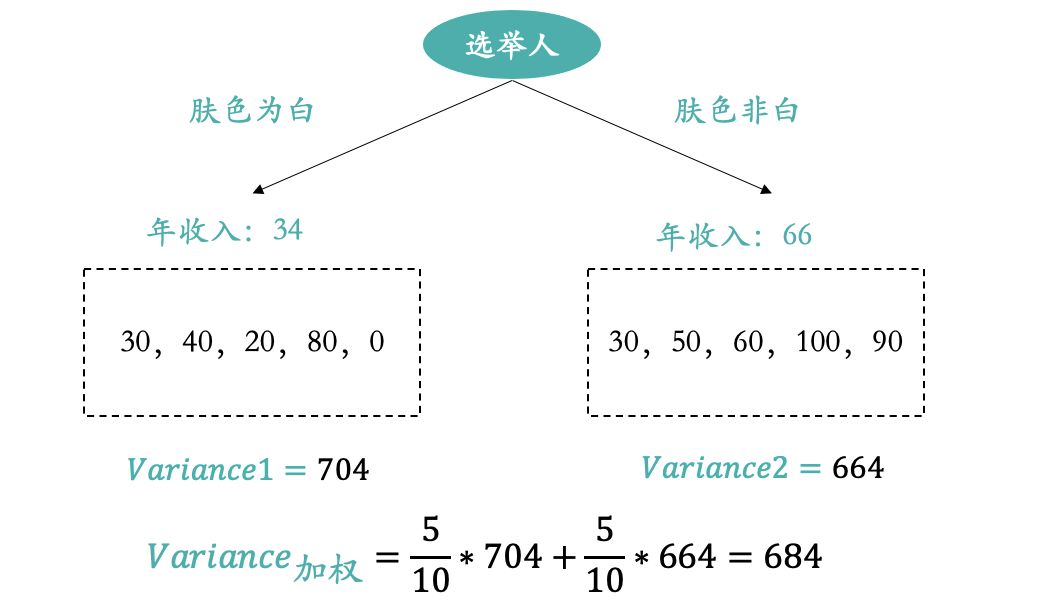
如上图,“肤色是否为白”作为输入变量,最终计算出的加权方差为684;所以在这两个输入变量中选择“选民选择的总统”作为输入变量更合适,因为该树模型对应的加权方差更小。
三、决策树模型的关键参数
上述三种方法介绍了如何选择输入变量,让决策树的分裂效果更好。同时我们在构建决策树模型时会设置一些关键的参数,去控制树的深度和叶子节点数量等等,主要是为了控制树模型过拟合,因为理论上不对决策树模型进行控制,决策树模型可以对训练样本达到100%的预测准确率,但这样就会严重过拟合。所以实际构建决策树模型时会有几个关键参数限制:

- 节点分裂包含的最小样本数:决策节点包含的样本数;过高,会导致模型欠拟合;过低又会导致模型过拟合;需要使用交叉检验的方式进行调参。
- 叶子节点包含的最小样本数:也是为了控制过拟合,如果样本数过小就会导致可以分出大量的叶子节点,所以会存在一个最小值限制。一般对于正负样本比例严重不均衡的分类,可以将此参数设置相对较小。
- 树的最大深度:深度过小,可能模型会欠拟合;深度过大,有可能模型会学习到一些特定样本才有的特征;需要使用交叉检验的方式进行调参。
- 总体的叶子节点数量:一般情况下,树深度为n的情况下,最多允许产生2^n个叶子节点。
- 整体分裂中使用的最多特征数:样本中数据会包含非常多的特征,从中挑选出哪些特征进行组合,进行分裂是构建树模型过程中非常重要的工作。根据建模经验,我们对总特征数开根号得出的特征数是最佳的特征数。使用过多特征会导致模型过拟合。
四、树模型剪枝
为了防止树模型过拟合,通常情况下我们需要对模型进行剪枝,剪枝方法一共有两种:
1. 预剪枝(Pre-pruning)
构造决策树模型的过程中,在对每个决策节点在分裂前进行预估,如果当前节点的分裂不能带来模型泛化能力的提升,则该节点不再分裂,直接标记为叶子节点。
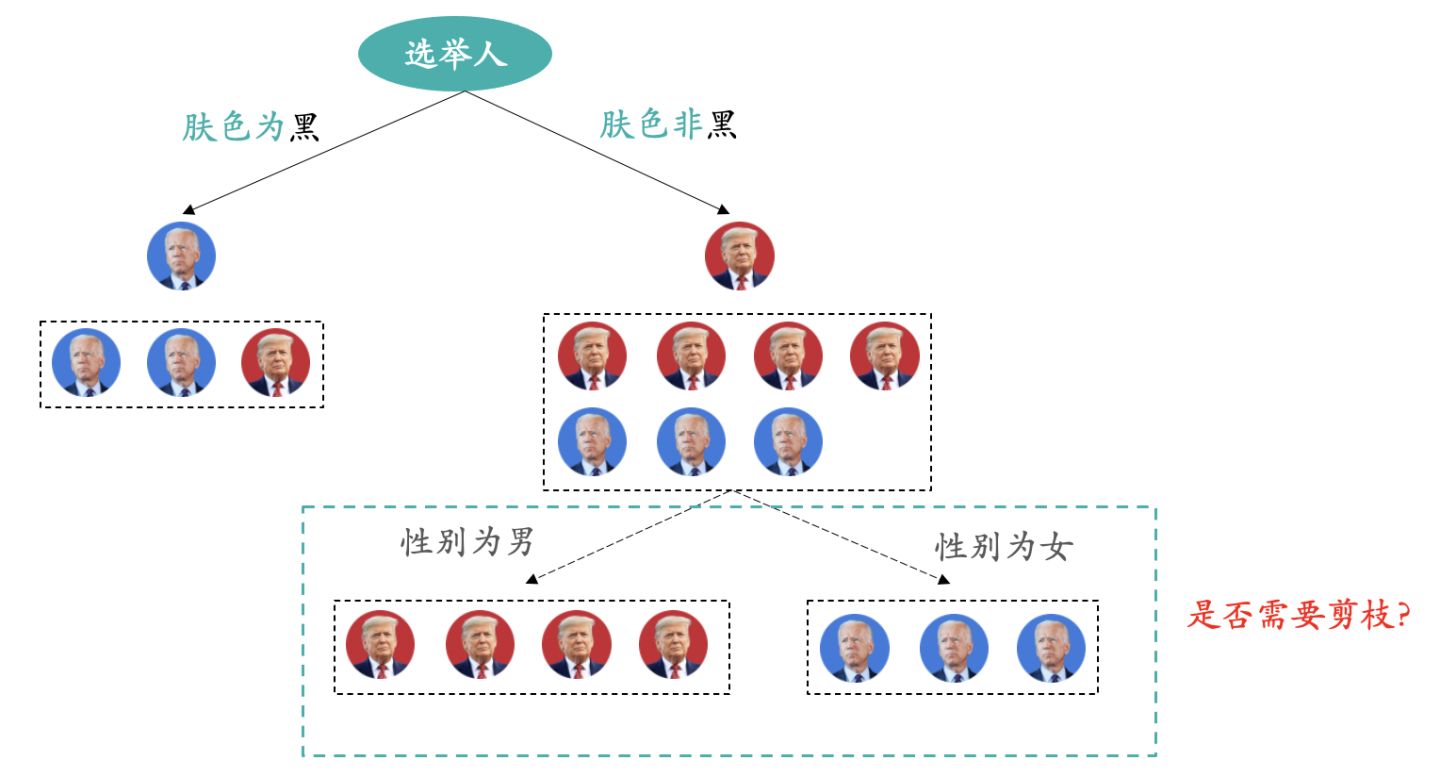
我们使用上图进行实例讲解,在对样本进行了“肤色是否为黑”的分裂后,针对右侧的节点判断是否要按照性别继续分裂。从训练集效果来看,按照性别分裂后效果是非常好的,新生成的叶子节点精准率均为100%。但是我们需要考虑模型的泛化能力,我们需要拿测试集来评估是否需要再分裂。注意我们所有的剪枝效果评估都是在测试样本上进行的,而不是训练样本!!!
假设测试集的样本为下面三条记录:

实施步骤:假设对该节点不进行分裂,模型预测“肤色非黑”即投票给川建国,因为案例是一个分类任务,所以我们使用精准率指标进行评估,Precision Rate = TP / (TP + FP)。测试样本中的精准率为50%;如果该节点按照性别进行分裂,模型预测“性别为男”投票川建国,“性别为女”投票拜振华,测试样本中的精准率表现为0%;分裂后,模型的泛化表现更差了。所以不建议分裂。
优缺点:预剪枝使得决策树的很多节点都没有“展开”,一方面降低了过拟合的风险和模型的训练时间。但另一方面,因为预剪枝是基于“贪心”的,虽然当前分裂不能提升泛化性能,但是基于该分裂的后续分裂却有可能导致效果提升,因此预剪枝策略有可能带来欠拟合的风险。
2. 后剪枝(Post-pruning)
后剪枝和预剪枝的策略完全反过来,在最开始分裂时先不考虑每次分裂在测试集上的效果表现,先尽可能地分裂。然后再自下而上地针对决策节点进行评估,如果将该决策节点下的所有叶子节点全部剪枝,将原本的决策节点变为新的叶子节点,是否在测试集上效果表现更好。
实施步骤:仍然是4.1里面的案例,按照性别分裂后的模型针对测试集的精准率为0;如果剪枝后,模型针对测试集的精准率变为50%,前后对比,所以建议剪枝。
优缺点:后剪枝策略通常会比预剪枝决策保留了更多的分支,因为前期尽可能地让树进行分裂。一般情形下,后剪枝决策树的欠拟合风险小,泛化能力也要优于预剪枝决策树。但后剪枝过程是在构建完全决策树之后进行的,并且要自底向上的对树中的所有非叶结点进行逐一考察,因此其训练时间要比未剪枝决策树和预剪枝决策树都大得多。
五、 连续值特征处理
在上述介绍时,“年收入”和“年龄”是一个连续值特征,针对这类连续值特征,我们不可能一个取值一个子节点,这样子节点太多了,我们如何选择出合理的分界点使其离散化。比如以年收入等于70万为一个分界线,但我们如何将70万这个值挑选出来呢?
通常情况对于连续值特征,我们会将所有的值从小到大进行排序,然后相邻的值之间取平均数。一个一个遍历所有的平均数将样本进行二分裂,计算出得到最小加权基尼不纯度的平均数,将该平均数作为我们最终连续值特征的分界点。

通常情况下连续值特征可以在一颗子树上重复使用,并不是一颗子树上只能使用该连续值特征分裂一次。比如父节点使用了“年收入小于等于70万”,子节点可以继续使用“年收入小于等于30万”分裂。
六、缺失值如何处理
很多时候现实中的数据,某些样本中的某个特征值缺失,缺失的原因可能是隐私或者历史丢失等原因。如果我们只使用完整的数据,可能训练样本量会比较少,所以现实中我们需要使用存在一定数据缺失的样本。那么这些样本怎么用?缺失值的使用存在两个问题:
我们继续使用该样本数据举例,肤色特征中有三条数据的肤色未知。

问题一解决方案:
首先我们仅使用该特征完善的样本计算熵、信息增益等,最后再乘以该部分样本站总样本的比例。比如针对肤色特征,上图数据一共只有7条完整数据,我们先用这7条完整数据计算“肤色”特征下的样本的总熵,然后按照已知的肤色取值“白”、“黄”、“黑”针对这7条数据分别分裂,分别计算各个节点的熵,再将这个节点的熵进行加权,然后计算信息增益,最终再乘以7/10。就是该特征在完整10条样本下的信息增益。详细计算过程如下图:

其他三个特征的处理方式和“肤色特征”处理方式完全一致,最后选择信息增益最大的特征进行分裂。
问题二解决方案:
假设我们选择了“肤色特征”进行分裂,那么对于肤色特征数据缺失的三条样本如何进行分裂了,该归属到哪个子节点里?实际处理时,该三条样本会同时进入三个分支里面:“白”、“黑”、“黄”。但是在三个分支里会分别有一个权重,“白”:2/7、“黑”:3/7、“黄”:2/7 。后续再对这些子节点再进行分裂时,计算熵、基尼不纯度等等,考虑该条样本的数据时都需要乘以此权重。其他特征取值缺失的数据处理方式是完全一样的。
那么上述就为大家详细介绍了如何构建决策树模型,如何选择特征,如何对树进行剪枝,缺失值如何处理等等。下一篇将为大家介绍一些经典的决策树模型,欢迎大家持续关注~
给作者点赞,鼓励TA抓紧创作!
来源:https://www.woshipm.com/pmd/5556982.html
本站部分图文来源于网络,如有侵权请联系删除。
 百木园
百木园