第三篇：基于计算图的神经网络的设计与实现

传送门： https://www.cnblogs.com/greentomlee/p/12314064.html

github: Leezhen2014: https://github.com/Leezhen2014/python_deep_learning

在第二篇中介绍了用数值微分的形式计算神经网络的梯度，数值微分的形式比较简单也容易实现，但是计算上比较耗时。本章会介绍一种能够较为高效的计算出梯度的方法：基于图的误差反向传播。

根据 deep learning from scratch 这本书的介绍，在误差反向传播方法的实现上有两种方法：一种是基于数学式的（第二篇就是利用的这种方法），一种是基于计算图的。这两种方法的本质是一样的，有所不同的是表述方法。计算图的方法可以参考feifei li负责的斯坦福大学公开课CS231n 或者theano的tutorial/Futher readings/graph Structures.

之前我们的误差传播是基于数学式的，可以看出对代码编写者来说很麻烦；

这次我们换成基于计算图的；

五、计算图

上一张我们实现了梯度下降算法，并且能训练出一个简单的神经网络了；本章会基于图计算的方式去实现神经网络。

P.S．：利用计算图的求导数的步骤类似于链式法则， 这里先挖个坑，稍后求sigmoid的微分的时候会举例。

5.1简单层的实现

Ps: 在前面的几章中，我对代码的重视程度并不大，这是因为前几章的涉及的代码都是作为理论基础。在后面的章节中会注意代码的组织结构。

在实现方面会尽量使用python的类。

为此，创建一个所有类的基类：BaseLayer

forward() 是推理过程中需要调用的函数；其内部的实现是基于公式本身。

backward() 是反向传播过程中需要调用的函数；其内部的实现是基于导数实现的。

以下是BaseLayer的具体实现方式。

  1 class BaseLayer:
  2     \'\'\'
  3     所有层的基类
  4     \'\'\'
  5     def forward(self,x,y):
  6         raise NotImplementedError
  7     def backward(self,dout):
  8         raise NotImplementedError
  9     def toString(self):
 10         raise NotImplementedError

为了能够更好的说明如何使用BaseLayer,我们给出乘法和加法的实现。

5.1.1 乘法层的实现

首先，乘法层的公式是：

反向传播的导数是：

；

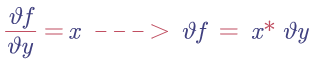其中， 和都是对x,y的微分；

• l我们将乘法层命名为 MulLayer, 这个层里面的forward() 是将两个矩阵相乘，x与y均为numpy.Ndarray类型；并且初始化self.x 与self.y
• backward() 是传入参数dout, dout是反向传播的梯度差，也是公式中的和， 因根据我们之前了解的梯度公式，可以知道反向传播的主要任务是更新权重，因此只需要将成员变量x,y的数值更新即可

  1 class MulLayer(BaseLayer):
  2     def __init__(self):
  3         self.x = None
  4         self.y = None
  5 
  6     def forward(self,x,y):
  7         self.x = x
  8         self.y = y
  9         out = x*y
 10 
 11         return out
 12 
 13     def backward(self,dout):
 14         \'\'\'
 15         反馈方面是反转x,y
 16         :param dout:
 17         :return:
 18         \'\'\'
 19         dx = dout * self.y
 20         dy = dout * self.x
 21         return  dx,dy
 22 
 23     def toString(self):
 24         print(\"name: Multi\")
 25         print(\"x.shape %s\"%str(self.x.shape))
 26         print(\"y.shape %s\"%str(self.y.shape))
 27 

5.1.2 加法层的实现

首先我们可以看看加法的公式：

其反向传播就是在对加法求导数，分别对x和y求导数后，其公式为：

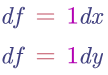
根据权重更新的公式，可知 x = dout *1 , y = dout*1

  1 class AddLayer(BaseLayer):
  2     def __init__(self):
  3         self.x = None
  4         self.y = None
  5 
  6     def forward(self,x,y):
  7         self.x = x
  8         self.y = y
  9         out = self.x+self.y
 10         return  out
 11     def backward(self,dout):
 12         dx = dout*1
 13         dy = dout*1
 14         return dx,dy
 15     def toString(self):
 16         print(\"name: Add\")
 17         print(\"x.shape %s\"%str(self.x.shape))
 18         print(\"y.shape %s\"%str(self.y.shape))

小结

本节给出了基于计算图的实现方法； 并结合反向传播机制，对乘法和加法的backward进行了实现。

我心匪石，不可转也。我心匪席，不可卷也。

来源：https://www.cnblogs.com/greentomlee/p/16686711.html
本站部分图文来源于网络，如有侵权请联系删除。