Python图像处理丨基于K-Means聚类的图像区域分割

摘要：本篇文章主要讲解基于理论的图像分割方法，通过K-Means聚类算法实现图像分割或颜色分层处理。

本文分享自华为云社区《[Python图像处理] 十九.图像分割之基于K-Means聚类的区域分割》，作者： eastmount。

本篇文章主要讲解基于理论的图像分割方法，通过K-Means聚类算法实现图像分割或颜色分层处理。基础性文章，希望对你有所帮助。

• 一.K-Means原理
• 二.K-Means聚类分割灰度图像
• 三.K-Means聚类对比分割彩色图像

注意 ：该部分知识均为杨秀璋查阅资料撰写，未经授权禁止转载，谢谢！！如果有问题随时私聊我，只望您能从这个系列中学到知识，一起加油喔~

该系列在github所有源代码：https://github.com/eastmountyxz/ImageProcessing-Python

一.K-Means聚类原理

第一部分知识主要参考自己的新书《Python网络数据爬取及分析从入门到精通（分析篇）》和之前的博客 [Python数据挖掘课程] 二.Kmeans聚类数据分析。

K-Means聚类是最常用的聚类算法，最初起源于信号处理，其目标是将数据点划分为K个类簇，找到每个簇的中心并使其度量最小化。该算法的最大优点是简单、便于理解，运算速度较快，缺点是只能应用于连续型数据，并且要在聚类前指定聚集的类簇数。

下面是K-Means聚类算法的分析流程，步骤如下：

• 第一步，确定K值，即将数据集聚集成K个类簇或小组。
• 第二步，从数据集中随机选择K个数据点作为质心（Centroid）或数据中心。
• 第三步，分别计算每个点到每个质心之间的距离，并将每个点划分到离最近质心的小组，跟定了那个质心。
• 第四步，当每个质心都聚集了一些点后，重新定义算法选出新的质心。
• 第五步，比较新的质心和老的质心，如果新质心和老质心之间的距离小于某一个阈值，则表示重新计算的质心位置变化不大，收敛稳定，则认为聚类已经达到了期望的结果，算法终止。
• 第六步，如果新的质心和老的质心变化很大，即距离大于阈值，则继续迭代执行第三步到第五步，直到算法终止。

下图是对身高和体重进行聚类的算法，将数据集的人群聚集成三类。

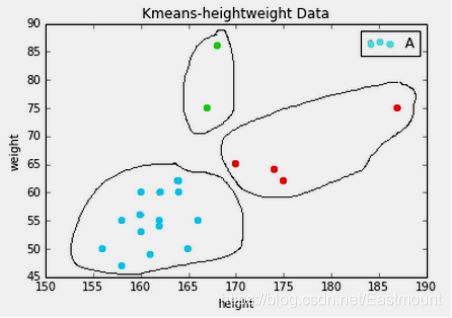
二.K-Means聚类分割灰度图像

在图像处理中，通过K-Means聚类算法可以实现图像分割、图像聚类、图像识别等操作，本小节主要用来进行图像颜色分割。假设存在一张100×100像素的灰度图像，它由10000个RGB灰度级组成，我们通过K-Means可以将这些像素点聚类成K个簇，然后使用每个簇内的质心点来替换簇内所有的像素点，这样就能实现在不改变分辨率的情况下量化压缩图像颜色，实现图像颜色层级分割。

在OpenCV中，Kmeans()函数原型如下所示：

retval, bestLabels, centers = kmeans(data, K, bestLabels, criteria, attempts, flags[, centers])

• data表示聚类数据，最好是np.flloat32类型的N维点集
• K表示聚类类簇数
• bestLabels表示输出的整数数组，用于存储每个样本的聚类标签索引
• criteria表示算法终止条件，即最大迭代次数或所需精度。在某些迭代中，一旦每个簇中心的移动小于criteria.epsilon，算法就会停止
• attempts表示重复试验kmeans算法的次数，算法返回产生最佳紧凑性的标签
• flags表示初始中心的选择，两种方法是cv2.KMEANS_PP_CENTERS ;和cv2.KMEANS_RANDOM_CENTERS
• centers表示集群中心的输出矩阵，每个集群中心为一行数据

下面使用该方法对灰度图像颜色进行分割处理，需要注意，在进行K-Means聚类操作之前，需要将RGB像素点转换为一维的数组，再将各形式的颜色聚集在一起，形成最终的颜色分割。

# coding: utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt
#读取原始图像灰度颜色
img = cv2.imread(\'scenery.png\', 0) 
print img.shape
#获取图像高度、宽度
rows, cols = img.shape[:]
#图像二维像素转换为一维
data = img.reshape((rows * cols, 1))
data = np.float32(data)
#定义中心 (type,max_iter,epsilon)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
#设置标签
flags = cv2.KMEANS_RANDOM_CENTERS
#K-Means聚类 聚集成4类
compactness, labels, centers = cv2.kmeans(data, 4, None, criteria, 10, flags)
#生成最终图像
dst = labels.reshape((img.shape[0], img.shape[1]))
#用来正常显示中文标签
plt.rcParams[\'font.sans-serif\']=[\'SimHei\']
#显示图像
titles = [u\'原始图像\', u\'聚类图像\'] 
images = [img, dst] 
for i in xrange(2): 
 plt.subplot(1,2,i+1), plt.imshow(images[i], \'gray\'), 
 plt.title(titles[i]) 
 plt.xticks([]),plt.yticks([]) 
plt.show()

输出结果如图所示，左边为灰度图像，右边为K-Means聚类后的图像，它将灰度级聚集成四个层级，相似的颜色或区域聚集在一起。

三.K-Means聚类对比分割彩色图像

下面代码是对彩色图像进行颜色分割处理，它将彩色图像聚集成2类、4类和64类。

# coding: utf-8
import cv2
import numpy as np
import matplotlib.pyplot as plt
#读取原始图像
img = cv2.imread(\'scenery.png\') 
print img.shape
#图像二维像素转换为一维
data = img.reshape((-1,3))
data = np.float32(data)
#定义中心 (type,max_iter,epsilon)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
#设置标签
flags = cv2.KMEANS_RANDOM_CENTERS
#K-Means聚类 聚集成2类
compactness, labels2, centers2 = cv2.kmeans(data, 2, None, criteria, 10, flags)
#K-Means聚类 聚集成4类
compactness, labels4, centers4 = cv2.kmeans(data, 4, None, criteria, 10, flags)
#K-Means聚类 聚集成8类
compactness, labels8, centers8 = cv2.kmeans(data, 8, None, criteria, 10, flags)
#K-Means聚类 聚集成16类
compactness, labels16, centers16 = cv2.kmeans(data, 16, None, criteria, 10, flags)
#K-Means聚类 聚集成64类
compactness, labels64, centers64 = cv2.kmeans(data, 64, None, criteria, 10, flags)
#图像转换回uint8二维类型
centers2 = np.uint8(centers2)
res = centers2[labels2.flatten()]
dst2 = res.reshape((img.shape))
centers4 = np.uint8(centers4)
res = centers4[labels4.flatten()]
dst4 = res.reshape((img.shape))
centers8 = np.uint8(centers8)
res = centers8[labels8.flatten()]
dst8 = res.reshape((img.shape))
centers16 = np.uint8(centers16)
res = centers16[labels16.flatten()]
dst16 = res.reshape((img.shape))
centers64 = np.uint8(centers64)
res = centers64[labels64.flatten()]
dst64 = res.reshape((img.shape))
#图像转换为RGB显示
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
dst2 = cv2.cvtColor(dst2, cv2.COLOR_BGR2RGB)
dst4 = cv2.cvtColor(dst4, cv2.COLOR_BGR2RGB)
dst8 = cv2.cvtColor(dst8, cv2.COLOR_BGR2RGB)
dst16 = cv2.cvtColor(dst16, cv2.COLOR_BGR2RGB)
dst64 = cv2.cvtColor(dst64, cv2.COLOR_BGR2RGB)
#用来正常显示中文标签
plt.rcParams[\'font.sans-serif\']=[\'SimHei\']
#显示图像
titles = [u\'原始图像\', u\'聚类图像 K=2\', u\'聚类图像 K=4\',
 u\'聚类图像 K=8\', u\'聚类图像 K=16\', u\'聚类图像 K=64\'] 
images = [img, dst2, dst4, dst8, dst16, dst64] 
for i in xrange(6): 
 plt.subplot(2,3,i+1), plt.imshow(images[i], \'gray\'), 
 plt.title(titles[i]) 
 plt.xticks([]),plt.yticks([]) 
plt.show()

输出结果如下图所示，当K=2颜色聚集成两种，当K=64颜色聚集成64种。

点击关注，第一时间了解华为云新鲜技术~

来源：https://www.cnblogs.com/huaweiyun/p/16673368.html
本站部分图文来源于网络，如有侵权请联系删除。