树结构

1.1 树的定义

树(Tree)：个节点构成的有限集合。当n = 0时，称为空树。对于任一棵非空树(n>0)，它具备以下性质：

树中有一个称为\"根(Root)\"的特殊节点，用r表示；其余节点可分为m(m>0)个互不相交的有限集、，...,，其中每个集合本身又是一棵树，称为原来树的子树(SubTree)。如下图：

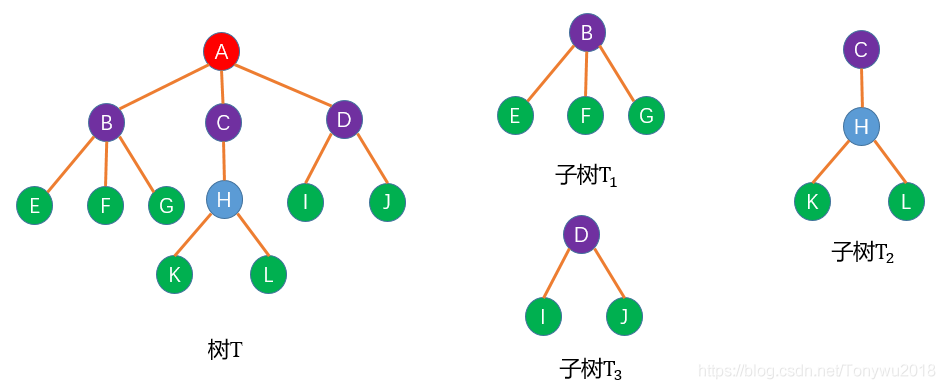
1.2 树结构的术语

树结构中有很多概念术语，在深入讨论树结构之前，我们先来介绍下跟树结构有关的术语。为了方便理解记忆，结合具体的一棵树结构来进行介绍，树结构如下：

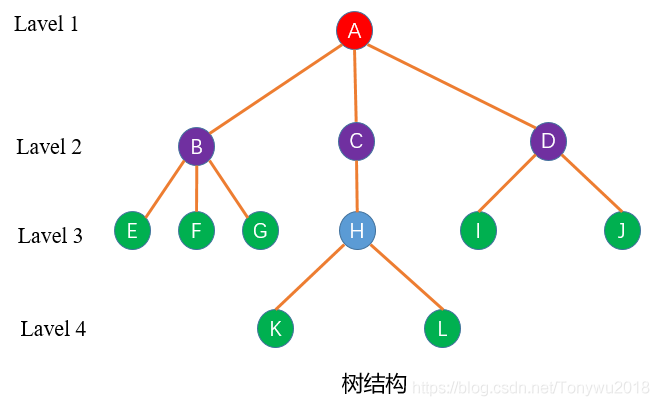
节点：树中存储的项。上图中的A-L都是节点。

根节点：树中最顶端的节点。在树结构中只有它没有父节点。上图中的A为根节点。

节点的度：一个节点含有的子树的个数。根节点A的度为3；子节点C的度为1。

树的度：树中最大节点度。树中最大节点度为3(根节点A和子节点B的度均为3)，所以树的度为3。

子节点(孩子节点)：紧邻一个给定的节点之下，并且直接与给定节点相连的一个节点。一个节点可以有多个子节点。上图中B-L都是子节点。

父节点(双亲节点)：紧邻一个给定节点之上，且直接与给定节点相连的一个节点。一个节点只能有一个父节点。上图中A、B、C、D、H都是父节点。

兄弟节点：拥有共同父节点的子节点。上图中B、C、D是兄弟节点，E、F、G也是兄弟节点。

叶子节点：没有子节点的节点。或者说度为0的节点。上图中标绿的几个节点都是叶子节点。

内部节点：至少有一个子节点的节点。B、C、D、H都是内部节点。

边/分支：将一个父节点连接到其子节点的线。上图中的线就是边也称为分支。

后代(子孙)：以某节点为根的子树中任一节点都称为该节点的后代。E、F、G是节点B的后代；H、K、L是节点C的后代，B-L的所有节点都是根节点A的后代。

祖先：从根到该节点所经分支上的所有节点。节点D是I、J的祖先；根节点A是所有节点的祖先。

路径：连接一个节点与其后代节点边的序列。A-B-E和A-C-H-K都可以称作一条路径。

路径长度：路径中边的数目。路径A-B-E的路径长度为2；路径A-C-H-K的路径长度为3。

节点的层次：从根节点定义，根节点为第1层，根节点的子节点为第2层，依次类推。节点的层在上图中已经标出。

深度(高度)：叶子节点所在的最大层次。上图中树的深度为4。

森林：m棵不相交的树的集合。分别以B、C、D为根节点的子树组成的集合可以看做一个森林。

以上就是树结构的一些术语。

1.3 树的分类

树结构可以分为两大类：有序树和无序树。树中任意节点间没有顺序关系，那么称其为无序树，也称自由树。相对的，树中的任意节点有顺序关系，称其为有序树。在有序树中，子节点被视为按照从左到右的顺序排列，最左边的子节点称为第一个子节点，最右边的子节点称为最后一个子节点。我们研究的最多的树结构就是有序树。而有序树中最具代表性的树结构就是二叉树。

二叉树就是度不超过2的有序树结构。 二叉树中的每个节点最多只能有两个分支，分别称为左子树和右子树。

根据二叉树的定义，会有如下两种极端的二叉树：

​

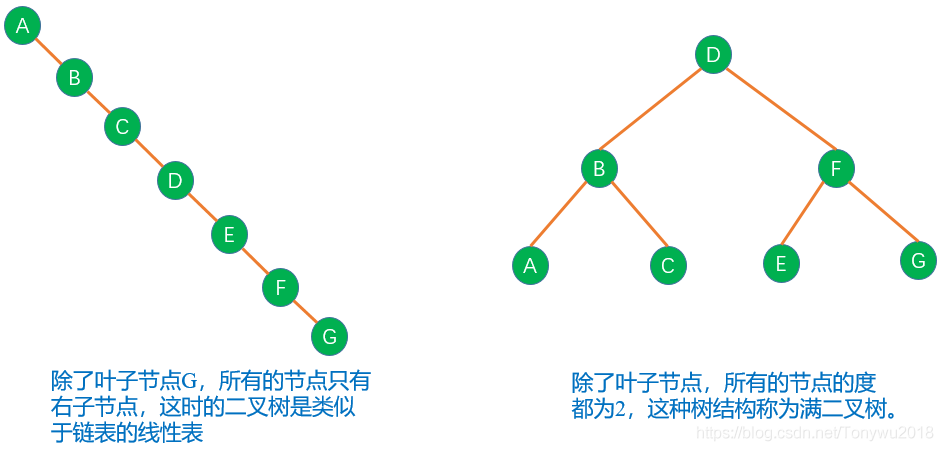
根据二叉树的形状，有以下几种常见的二叉树：

平衡二叉树：当且仅当任意节点的两棵子树的高度差不大于1的二叉树。

完全二叉树：除了最后一层外，其他层的节点数目都达到最大的二叉树。完全二叉树是平衡二叉树的一个特例，完全二叉树最后一层上的节点都是从左到右填充的。对于一颗k层的完全二叉树，其节点总数最少的情况是：最后一层只有一个节点，此时节点数目为：；其节点总数最多的情况是：最后一层节点数目达到最大，即满二叉树，此时节点数目为：。对于节点数目为k的完全二叉树，其深度为：

满二叉树：所有层的节点数目均达到最大的二叉树。满二叉树是完全二叉树的一个特例。对于深度为k的满二叉树，其节点数目是：；对于节点数目为k的满二叉树，其深度为：。

几种二叉树的结构图如下：

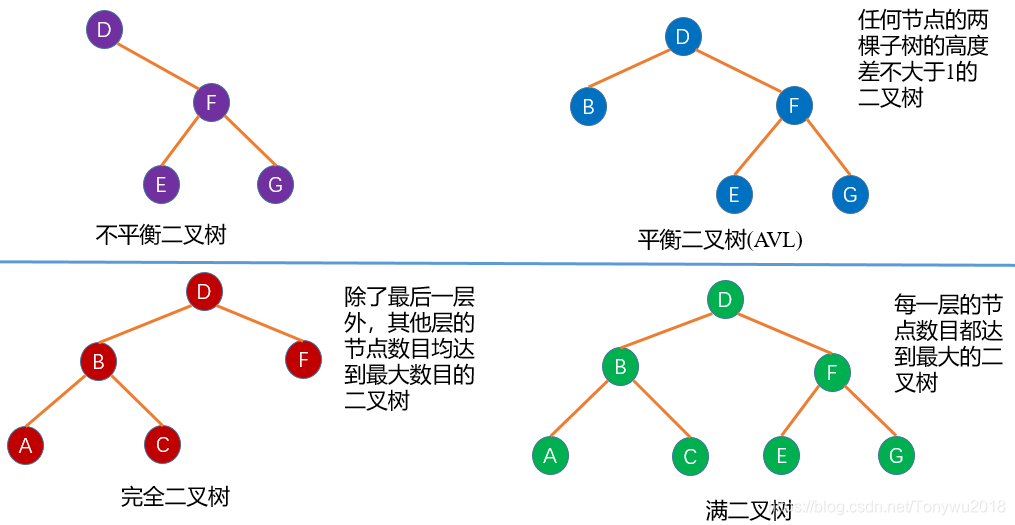
关于二叉树还有一个性质：二叉树中叶子节点数为(因为叶子节点的度为0，所以下标为0)，度为2的节点数为 ，那么有: n₀ = n₂ + 1

解析：关于上面等式关系的求解我们可以这样考虑。假设二叉树的总节点数为，因为二叉树的节点度只有0、1、2三种情况，假设节点度为0、1、2的节点数分别为：n₀、n₁和n₂。那么有n = n₀ + n₁ + n₂。二叉树中节点度为1的节点有1条边连接到其子节点、节点度为2的节点有2条边连接到其子节点，假设二叉树有E条边，那么E = n₁ + 2n₂。而我们知道，在二叉树中节点总数和边的数目有这样的关系：n = E +1 = n₁ + 2n₂ + 1。联立加粗的两个等式，容易得出 n₀ = n₂ + 1。

来源：https://www.cnblogs.com/minqiliang/p/16825403.html
本站部分图文来源于网络，如有侵权请联系删除。