最小生成树之普利姆算法与克鲁斯卡尔算法（贪心算法）

最小生成树（贪心算法）

概念

• 一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。
• 连通图有多种连接方式，而其中最小的连通图，就是最小生成树
• 连通图分为：无向、有向
  • 无向连通图：所以顶点相连，但各个边都没有方向
  • 有向连通图：边有方向

1.普利姆算法（Prim）-----最近顶点策略

• 策略：选择图中的一个顶点作为起始点，每一步贪心选择不在当前生成树中的最近顶点加入生成树中，直到所有顶点都加入到树中。

• 算法如下：

  （1）、假如G为无向连通带权图，每两个相邻节点构成一个带权边，其值设为：权值。即:(所有每相邻的两个节点都有各自的权值，只是权值大小不同)

  （2）、设集合 W和D，W用于存放G的最小生成树的顶点集合，D存放G的最小生成树的权值集合

  （3）、选中G的一个节点 (其索引为data-0) 作为初值，从顶点data0开始构建最小生成树。集合D的初值为D{}。

  （4）、标记W[data0]=1.表示标记已被选中的节点

  （5）、data0节点找出周围相邻，且带权边最小的节点(其索引为data-n)。

  （6）、将节点data-n加入集合W。标记W[data-n]=1;将带权边(data0,data-n)加入集合D

  （7）、重复上面步骤

• 图解步骤：

  （1）、无向连通图

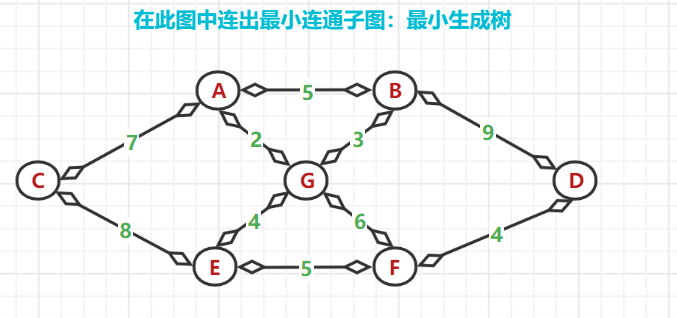
（2）、以节点A开始延申：发现（A,G）间的权值最小，于是选中G为连通点

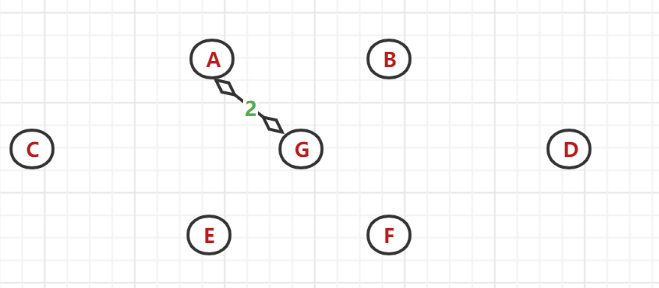
（3）、以A、G节点为顶点找与之相邻的最小权值边：发现（G,B）间的带权边值最小，选中B

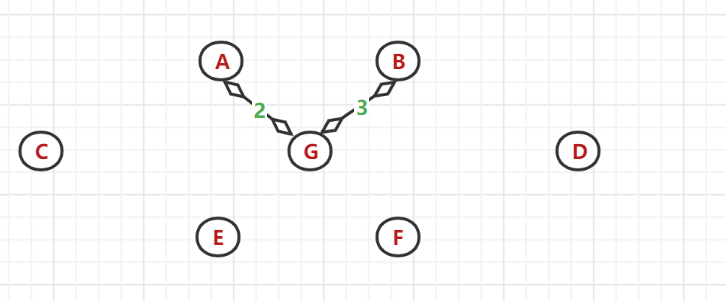
（4）、又以 A、G、B节点为顶点找与之相邻的最小权值边：发现（G,E）间的带权边值最小，选中E

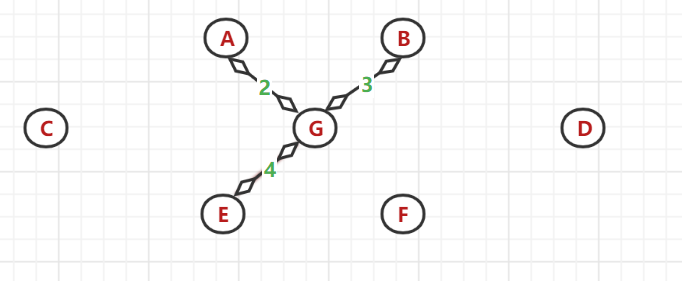
（5）、又以 A、G、B、E节点为顶点找与之相邻的最小权值边：发现（B,A）与（E,F）间的带权边值最相同且最小，但A和B节点都是已使用过的节点，所以选中 F 节点

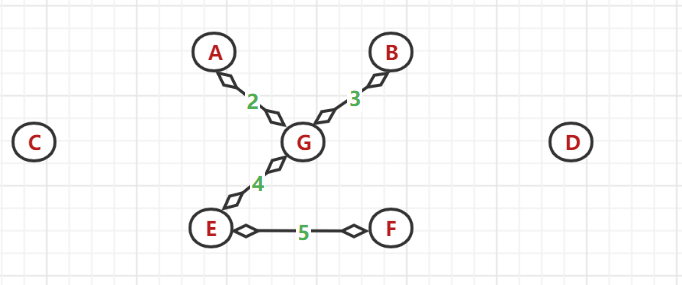
（6）、依次选择，得到最后的最小生成树

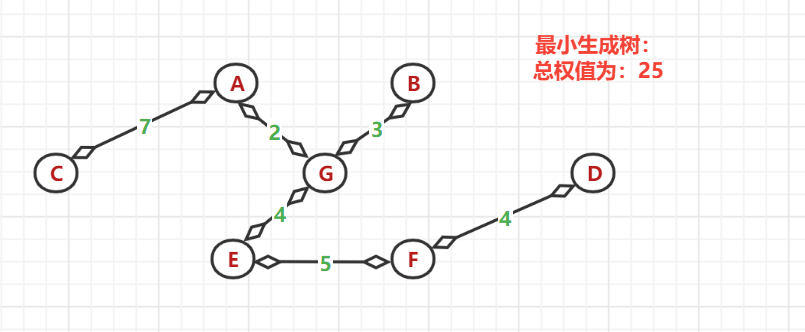
代码如下：

import java.util.Arrays;

/*
贪心策略：最小生成树-普里姆算法
       ：在包含n个顶点的无向连通图中，找出只有（n-1）条边且包含n个顶点的连通子图。使其形成最小连通子图。连通子图不能出现回路
分析：
    1.设置集合 W和集合 D 。其中W存入的是无向连通图中最小生成树的顶点集合；D存入的是最小生成树每相邻两个顶点之间的连接边的集合
    2.另集合W的初值为 W{w0}(即从w0顶点开始构建最小生成树)，另集合D初始值为 D{}
    3.设V为还未被选中的顶点。
    4.从w与v=V-W 中组成的所有带权边中选出最小的带权边(wn,vn).
    5.将顶点vn加入集合W中。此时集合W{wn,vn},集合D{(wn,vn)}
    6.重复上面步骤，直到V中所有顶点都加入到了W中，边有n-1条带权边。结束
代码：探讨修路问题
 */
public class test1 {
    public static void main(String[] args) {
        //所有节点
    char[] ndata=new char[]{\'A\',\'B\',\'C\',\'D\',\'E\',\'F\',\'G\'};
        //获取节点个数
        int nodes = ndata.length;
        //邻接矩阵.用较大的数10000表示两点不连通
        int[][] ndlenght=new int[][]{
                //A   ,B,C,  D  ,  E  ,  F  ,G
                {10000,5,7,10000,10000,10000,2},    //A
                {5,10000,10000,9,10000,10000,3},    //B
                {7,10000,10000,10000,8,10000,10000},//C
                {10000,9,10000,10000,10000,4,10000},//D
                {10000,10000,8,10000,10000,5,4},    //E
                {10000,10000,10000,4,5,10000,6},    //F
                {2,3,10000,10000,4,6,10000},        //G
                                                };
        //创建图对象
        Chart chart=new Chart(nodes);
        //创建生成数对象
        MinTree mt=new MinTree();
        //创建邻接矩阵
        mt.creathart(chart,nodes,ndata,ndlenght);
        //获取矩阵
       // mt.dischart(chart);
        mt.Prim(chart,0);


    }

}

/*
第二步：
创建生成树对象
 */
class MinTree{
    /**
     * 创建邻接矩阵
     * @param chart :图对象
     * @param nodes ：节点个数
     * @param ndata :存放节点数据
     * @param ndlenght  :带权边
     */
    public void creathart(Chart chart,int nodes,char[] ndata,int[] [] ndlenght){
        //i:已经被选中的节点，ndata[i0]就是为初值，ndata[0]节点开始生成树。一共有nodes个
        for (int i=0;i<nodes;i++){
            //将当前已被选的节点存入图对象的ndata中
            chart.ndata[i]=ndata[i];
            //j:还未被选中的节点
            for (int j=0;j<nodes;j++){
                //将所有可能两两连接的节点组合，存入图对象的邻接矩阵中
                chart.ndlenght[i][j]=ndlenght[i][j];
            }
        }
    }

    //显示图矩阵
    public void dischart(Chart chart){
        for (int[] link:chart.ndlenght){
            System.out.println(Arrays.toString(link));
        }
    }


    /**
     * 普里姆算法:
     *    最小生成树
     * @param chart:图
     * @param v :初值
     */
    public void Prim(Chart chart,int v){
        //存放已被选中的节点，初始都为0
        int[] ondata=new int[chart.nodes];
        //标记初值节点已被选中,1(表示被选中了的)
        ondata[v]=1;
        //设即将相连的两个节点下标为 index1、index2。由于还没有存入，所以初始为-1
        int index1=-1;
        int index2=-1;
        //由于还不知道第一个边长为多少，所以先虚拟设置一个最大带权边长。后面后被替换的
        int max=10000;
        //k:表示最多生成（n-1)条带权边
        for (int k=1;k<chart.nodes;k++){
            //i:表示以被选中的节点；j:还未被选中的节点
            for (int i=0;i<chart.nodes;i++){
                for (int j=0;j<chart.nodes;j++){
                    if (ondata[i]==1&&ondata[j]==0&&chart.ndlenght[i][j]<max){
                        max=chart.ndlenght[i][j];
                        index1=i;
                        index2=j;
                    }
                }
            }
            System.out.println(\"节点:<\"+chart.ndata[index1]+\",\"+chart.ndata[index2]+\">,==>带权边长:\"+max);
            //将当前节点标记为以访问使用的节点
            ondata[index2]=1;
            //重置max
            max=10000;
        }

    }

}

/*
第一步：
创建图对象
 */
class Chart{
    int nodes;  //图中节点个数
    char[] ndata;   //存放节点数据
    int[] [] ndlenght;  //存放带权边。也是邻接矩阵

    //构造器
    public Chart(int nodes) {
        this.nodes = nodes;
        //初始化，数组长度为nodes(节点个数)
        ndata=new char[nodes];
        //初始化，矩阵为nodes行nodes列
        ndlenght=new int[nodes][nodes];
    }
}

结果：

2.,克鲁斯卡尔算法(Kruskal)----最短边策略

• 策略：每一次贪心的选择从剩下的边中最小的边且不产生环路的，加入到已选边的集合中。直到所有顶点都加入进来。

• 按照权值从小到大选择n-1条边，并且这些边不构成环路。

• 算法如下：

  （1）、构建有n个顶点的无边连通图 W ，

  （2）、对无向连通图 H 中的各个带权边从小到大排序

  （3）、依次从小到大将 H 中的带权边加入到 W中（期间不能构成环路）

• 算法图解及判断环路：

  • 环路：已加入加入到无边联通图中的顶点的终点不能相同

  • 终点：将所有顶点从小到大排序后，某个顶点的终点就是\"与它相连的最大的顶点\";

  • （1）、无边连通图 W。与无向连通图 H（1:顶点以排序;2.权值以排序）

    • 顶点的终点：此时由于还没有加入。所以W中所有的各个顶点的终点是自己本身

  ​

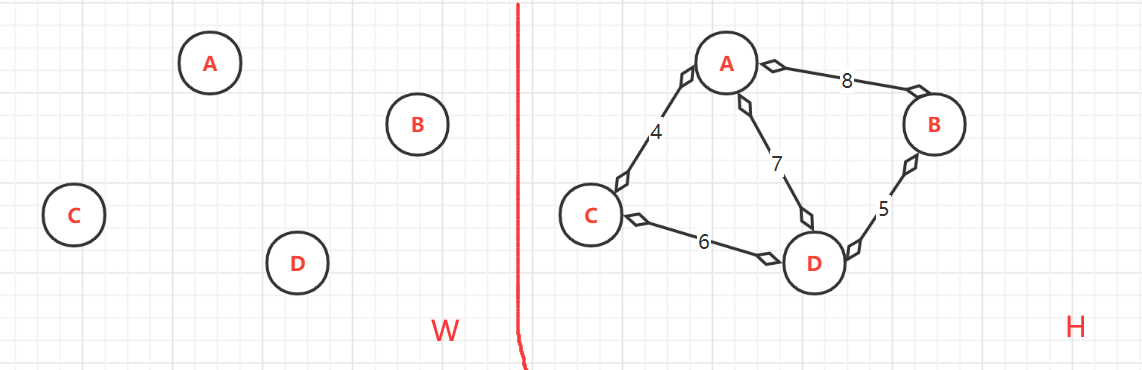
• （2）、将H中从小到大排序后的边依次加入 W中。

  • （2.1）、第一次：<A,C>=4，

  • 顶点的终点：因为顶点是已排序为{A,B,C,D},而目前加入到W中的只有{A，C}。所以A与C连通的最大顶点是：A--->C;C--->C

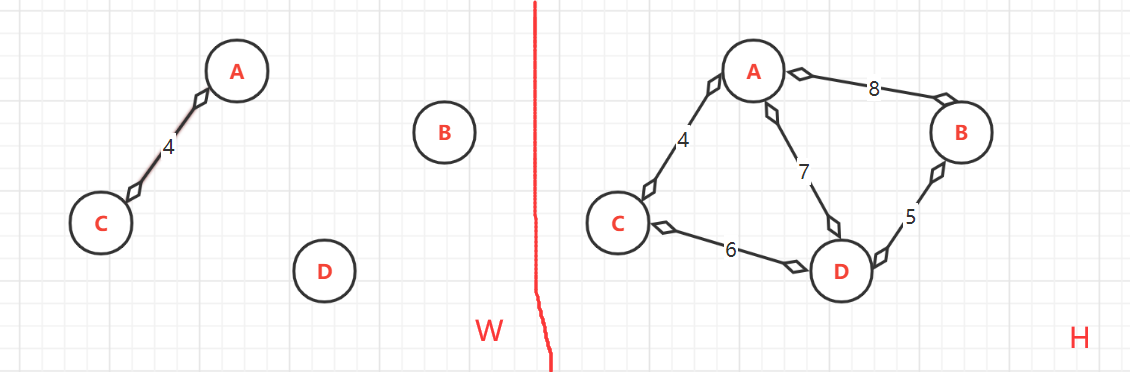
- （2.2）、第二次：<B,D>=5，

- 顶点的终点：此时**W**中有{A，C}，{B，D}。由于目前{B，D}还没有与{A，C}连通，所以B与D连通的最大顶点是：B--->D;D--->D,

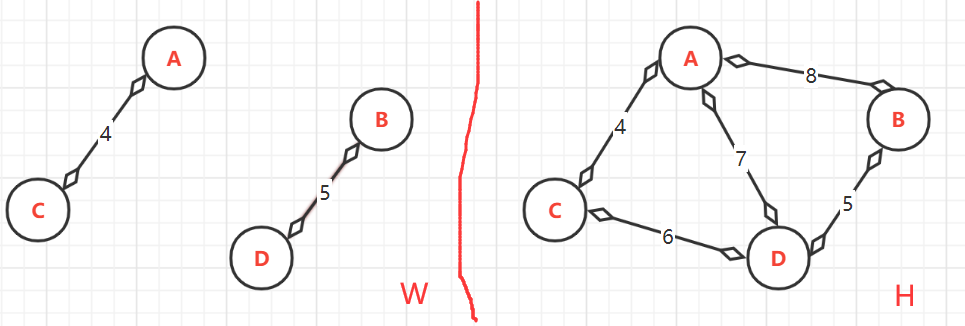
- （2.3）、第三次：<C,D>=6，这里虽然前面C与D被加入过，但它们的终点却不同。

- 顶点的终点：此时**W**中有{A，C}，{B，D}，{C，D}。由于{C，D}的加入导致{A,B,C,D}相互连接，所最大顶点是：A--->D;B--->D;C--->D;D--->D,

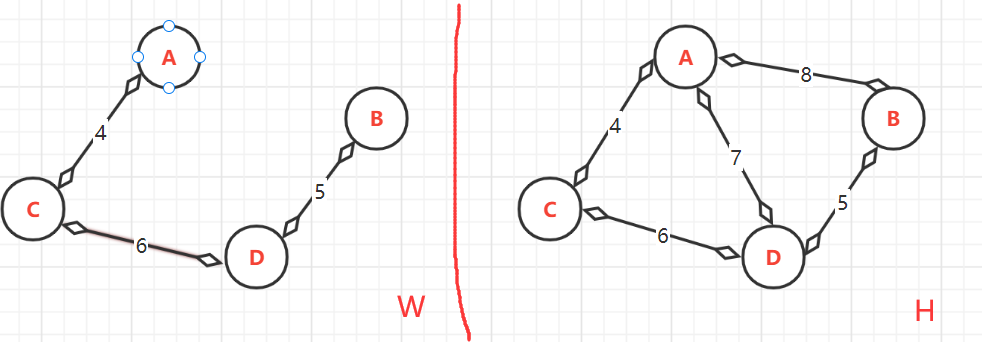
- （2.4）、第四次：<A,D>=7。由于前面得出A，与D的最大顶点(终点)相同为D，如果加入会构成环路。所以不能加入.跳过此边，加入下一条边

- （2.5）、第五次：<A,B>=8。由于前面得出A，与B的最大顶点(终点)相同为D，如果加入会构成环路。所以不能加入。所以加入下一条边，发现没有，所有边都已加入到了。

• （3）、注意：在（2.3）时。其实所有顶点都已加入到了W中，所以就不需要判断后面的了。后面的结论只是为了说明终点与环路。

• 代码如下：

import java.util.Arrays;

/**
 * 最小生成树：克鲁斯卡尔算法
 * 将无向连通图中的各个边从小到大排序，依次放入无边连通图中（不能出现环路）
 */
public class test1 {

    private int geshu;  //边的个数
    private char[] data; //存放节点
    private int[][] allquanzhi;   //存放带权边，邻接矩阵
    //标记不能相连通的两个节点，即不相邻的两个节点所形成的带权边。为Integer最大值
    private static final int maxlen = Integer.MAX_VALUE;

    public static void main(String[] args) {
      //  char[] data={\'A\',\'B\',\'C\',\'D\',\'E\'};
//        int[][] allquanzhi={
//                {0,20,maxlen,60,15},
//                {20,0,42,maxlen,maxlen},
//                {maxlen,42,0,30,maxlen},
//                {60,maxlen,30,0,23},
//                {15,maxlen,maxlen,23,0},
//                };
        char[] data={\'A\',\'B\',\'C\',\'D\'};
        int[][] allquanzhi={
                {0,8,4,7},
                {8,0,maxlen,5},
                {4,maxlen,0,6},
                {7,5,6,0}
                    };
        test1 t=new test1(data,allquanzhi);
        //打印矩阵
        t.dayinjuzheng();
        Bian[] bians=t.andbian();
        System.out.println(\"排序前的边集合\"+Arrays.toString(bians));
        t.biansort(bians);
        System.out.println(\"排序后的边集合\"+Arrays.toString(bians));
        t.KrusKal();

    }

    //定义构造器
    public test1(char[] data, int[][] allquanzhi) {
        //初始化顶点数
        int spotgeshu = data.length;
        //初始化顶点（节点）
        this.data = data;
        //初始化 边
        this.allquanzhi = allquanzhi;
        //统计边的个数
        for (int i = 0; i < spotgeshu; i++) {
            for (int j = i+1; j < spotgeshu; j++) {
                if (this.allquanzhi[i][j] < maxlen) {
                    geshu++;
                }
            }
        }
    }

    //打印邻接矩阵
    public void dayinjuzheng() {
        System.out.println(geshu);
        for (int i = 0; i < data.length; i++) {
            for (int j = 0; j < data.length; j++) {
                //格式化输出
                System.out.printf(\"%15d\\t\", +allquanzhi[i][j]);
            }
            System.out.println();
        }
    }


    /*
    对边排序：冒泡《从小到大》
     */
    public void biansort(Bian[] bian){
        for (int i=bian.length-1;i>0;i--){
            for (int j=0;j<i;j++){
                if (bian[j].bianquanzhi>bian[j+1].bianquanzhi){
                    Bian temp=bian[j];
                    bian[j]=bian[j+1];
                    bian[j+1]=temp;
                }
            }
        }
    }

    /*
    判断顶点是否存在
    返回顶点的索引
     */
public  int ismbian(char ch){
    for (int i=0;i<data.length;i++){
        if (data[i]==ch){
            return i;
        }
    }
    //如果ch不是顶点就返回-1
    return -1;
}

/*
将所以相邻边存入Bian[]中
 */
public Bian[] andbian(){
    int index=0;
    Bian[] bians=new Bian[geshu];
    for (int i=0;i<data.length;i++){
        for (int j=i+1;j<data.length;j++){
            if (allquanzhi[i][j]!=maxlen){
                bians[index++]=new Bian(data[i],data[j],allquanzhi[i][j]);
            }
        }
    }
    return bians;
}


/*
获取小标为i的顶点的终点，用于判断两个顶点的终点是否相同
star:存入的是顶点的终点的索引，初始化为{0，0，0，0，...},
i:顶点的索引
 */
public int getEnd(int[] star,int i){
    //动态的判断以此顶点的索引，
    //相连的前一个顶点的终点索引就是后一个顶点的索引
    //由于第一次的顶点的终点是自己的索引都
    //如果在star中找到了终点
    while (star[i]!=0){
        //就将此终点的值变为新的顶点的索引（找到此索引对应的顶点的终点，直到新的索引在star中没有找到终点，即为0，就将此索引返回为最初始的节点的终点索引）
        i=star[i];
    }
    //返回为终点
    return  i;
}


/*
最小生成树克鲁斯卡尔算法
 */
public  void KrusKal(){
    int index=0;    //最后结果数组的索引
    //存放最小生成树每个顶点的终点
    int[] star=new  int[geshu];
    //保存最终生成树
    Bian[] fin=new  Bian[geshu];
    //获取边的集合
    Bian[] andnewbian = andbian();
    //对所有边进行排序
    biansort(andnewbian);
    //遍历边集合。在判断的同时判断是否形成回路
    for (int i=0;i<geshu;i++){
        //上面andbian存放获得的边的类：bians[index++]=new Bian(data[i],data[j],allquanzhi[i][j]);
        //获取第一边的起点（顶点）,对应的是data[i]
        int h1=ismbian(andnewbian[i].da1);
        //获取第一条边的第二个顶点,对应的是data[j]
        int h2=ismbian(andnewbian[i].da2);
        //获取第一个顶点的终点
        int end = getEnd(star, h1);
        //获取第二个顶点的终点
        int end1 = getEnd(star, h2);
        //判断回路:如果没有构成回路
        if (end!=end1){
            //设置end1为已有生成数的终点
            star[end]=end1;
            //此时最终生成树有了一条边
            fin[index++]=andnewbian[i];
        }
    }
    System.out.println(\"最后生成树：\"+Arrays.toString(fin));
    System.out.println(\"最小生成树:\");
    for (int i=0;i<index;i++){
        System.out.println(fin[i]);
    }
}

}


/*
边类
 */
class Bian{
    //组成一条边的两个节点
    char da1;
    char da2;
    //边权值
    int bianquanzhi;

    public Bian(char da1, char da2, int bianquanzhi) {
        this.da1 = da1;
        this.da2 = da2;
        this.bianquanzhi = bianquanzhi;
    }

    @Override
    public String toString() {
        return \"bian{\" +
                \"da1=\" + da1 +
                \", da2=\" + da2 +
                \", bianquanzhi=\" + bianquanzhi +
                \'}\';
    }
}

结果：

来源：https://www.cnblogs.com/sazxj/p/16916851.html
本站部分图文来源于网络，如有侵权请联系删除。