集成学习投票法与bagging
投票法
sklearn提供了VotingRegressor和VotingClassifier两个投票方法。使用模型需要提供一个模型的列表,列表中每个模型采用tuple的结构表示,第一个元素代表名称,第二个元素代表模型,需要保证每个模型拥有唯一的名称。看下面的例子:
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
models = [(\'lr\',LogisticRegression()),(\'svm\',SVC())]
ensemble = VotingClassifier(estimators=models) # 硬投票
models = [(\'lr\',LogisticRegression()),(\'svm\',make_pipeline(StandardScaler(),SVC()))]
ensemble = VotingClassifier(estimators=models,voting=\'soft\') # 软投票
我们可以通过一个例子来判断集成对模型的提升效果。
首先我们创建一个1000个样本,20个特征的随机数据集合:
from sklearn.datasets import make_classification
def get_dataset():
X, y = make_classification(n_samples = 1000, # 样本数目为1000
n_features = 20, # 样本特征总数为20
n_informative = 15, # 含有信息量的特征为15
n_redundant = 5, # 冗余特征为5
random_state = 2)
return X, y
补充一下函数make_classification的参数:
- n_samples:样本数量,默认100
- n_features:特征总数,默认20
- n_imformative:信息特征的数量
- n_redundant:冗余特征的数量,是信息特征的随机线性组合生成的
- n_repeated:从信息特征和冗余特征中随机抽取的重复特征的数量
- n_classes:分类数目
- n_clusters_per_class:每个类的集群数
- random_state:随机种子
使用KNN模型来作为基模型:
def get_voting():
models = list()
models.append((\'knn1\', KNeighborsClassifier(n_neighbors=1)))
models.append((\'knn3\', KNeighborsClassifier(n_neighbors=3)))
models.append((\'knn5\', KNeighborsClassifier(n_neighbors=5)))
models.append((\'knn7\', KNeighborsClassifier(n_neighbors=7)))
models.append((\'knn9\', KNeighborsClassifier(n_neighbors=9)))
ensemble = VotingClassifier(estimators=models, voting=\'hard\')
return ensemble
为了显示每次模型的提升,加入下面的函数:
def get_models():
models = dict()
models[\'knn1\'] = KNeighborsClassifier(n_neighbors=1)
models[\'knn3\'] = KNeighborsClassifier(n_neighbors=3)
models[\'knn5\'] = KNeighborsClassifier(n_neighbors=5)
models[\'knn7\'] = KNeighborsClassifier(n_neighbors=7)
models[\'knn9\'] = KNeighborsClassifier(n_neighbors=9)
models[\'hard_voting\'] = get_voting()
return models
接下来定义下面的函数来以分层10倍交叉验证3次重复的分数列表的形式返回:
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
def evaluate_model(model, X, y):
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state = 1)
# 多次分层随机打乱的K折交叉验证
scores = cross_val_score(model, X, y, scoring=\'accuracy\', cv=cv, n_jobs=-1,
error_score=\'raise\')
return scores
接着来总体调用一下:
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
X, y = get_dataset()
models = get_models()
results, names = list(), list()
for name, model in models.items():
score = evaluate_model(model,X, y)
results.append(score)
names.append(name)
print(\"%s %.3f (%.3f)\" % (name, score.mean(), score.std()))
plt.boxplot(results, labels = names, showmeans = True)
plt.show()
knn1 0.873 (0.030)
knn3 0.889 (0.038)
knn5 0.895 (0.031)
knn7 0.899 (0.035)
knn9 0.900 (0.033)
hard_voting 0.902 (0.034)
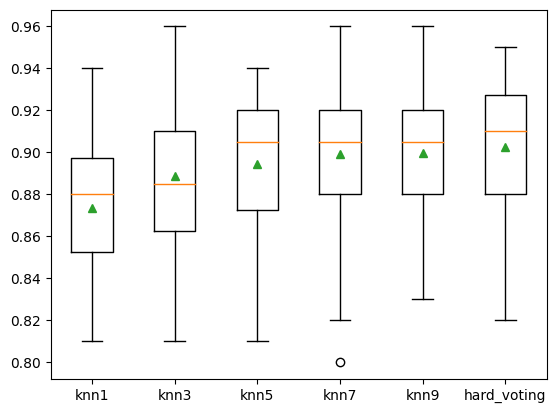
可以看到结果不断在提升。
bagging
同样,我们生成数据集后采用简单的例子来介绍bagging对应函数的用法:
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
model = BaggingClassifier()
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring=\'accuracy\', cv=cv, n_jobs=-1, error_score=\'raise\')
print(\'Accuracy: %.3f (%.3f)\' % (mean(n_scores), std(n_scores)))
Accuracy: 0.861 (0.042)
Boosting
关于这方面的理论知识的介绍可以看我这篇博客。
这边继续关注这方面的代码怎么使用。
Adaboost
先导入各种包:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use(\"ggplot\")
%matplotlib inline
import seaborn as sns
# 加载训练数据:
wine = pd.read_csv(\"https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data\",header=None)
wine.columns = [\'Class label\', \'Alcohol\', \'Malic acid\', \'Ash\', \'Alcalinity of ash\',\'Magnesium\', \'Total phenols\',\'Flavanoids\', \'Nonflavanoid phenols\',
\'Proanthocyanins\',\'Color intensity\', \'Hue\',\'OD280/OD315 of diluted wines\',\'Proline\']
# 数据查看:
print(\"Class labels\",np.unique(wine[\"Class label\"]))
wine.head()
Class labels [1 2 3]

那么接下来就需要对数据进行预处理:
# 数据预处理
# 仅仅考虑2,3类葡萄酒,去除1类
wine = wine[wine[\'Class label\'] != 1]
y = wine[\'Class label\'].values
X = wine[[\'Alcohol\',\'OD280/OD315 of diluted wines\']].values
# 将分类标签变成二进制编码:
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
y = le.fit_transform(y)
# 按8:2分割训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=1,stratify=y) # stratify参数代表了按照y的类别等比例抽样
这里补充一下LabelEncoder的用法,官方给出的最简洁的解释为:
Encode labels with value between 0 and n_classes-1.
也就是可以将原来的标签约束到[0,n_classes-1]之间,1个数字代表一个类别。其具体的方法为:
-
fit、transform:
le = LabelEncoder() le = le.fit([\'A\',\'B\',\'C\']) # 使用le去拟合所有标签 data = le.transform(data) # 将原来的标签转换为编码 -
fit_transform:
le = LabelEncoder() data = le.fit_transform(data) -
inverse_transform:根据编码反向推出原来类别标签
le.inverse_transform([0,1,2]) # 输出[\'A\',\'B\',\'C\']
继续AdaBoost。
我们接下来对比一下单一决策树和集成之间的效果差异。
# 使用单一决策树建模
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(criterion=\'entropy\',random_state=1,max_depth=1)
from sklearn.metrics import accuracy_score
tree = tree.fit(X_train,y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train,y_train_pred)
tree_test = accuracy_score(y_test,y_test_pred)
print(\'Decision tree train/test accuracies %.3f/%.3f\' % (tree_train,tree_test))
Decision tree train/test accuracies 0.916/0.875
下面对AdaBoost进行建模:
from sklearn.ensemble import AdaBoostClassifier
ada = AdaBoostClassifier(base_estimator=tree, # 基分类器
n_estimators=500, # 最大迭代次数
learning_rate=0.1,
random_state= 1)
ada.fit(X_train, y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train,y_train_pred)
ada_test = accuracy_score(y_test,y_test_pred)
print(\'Adaboost train/test accuracies %.3f/%.3f\' % (ada_train,ada_test))
Adaboost train/test accuracies 1.000/0.917
可以看见分类精度提升了不少,下面我们可以观察他们的决策边界有什么不同:
x_min = X_train[:, 0].min() - 1
x_max = X_train[:, 0].max() + 1
y_min = X_train[:, 1].min() - 1
y_max = X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))
f, axarr = plt.subplots(nrows=1, ncols=2,sharex=\'col\',sharey=\'row\',figsize=(12, 6))
for idx, clf, tt in zip([0, 1],[tree, ada],[\'Decision tree\', \'Adaboost\']):
clf.fit(X_train, y_train)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
axarr[idx].contourf(xx, yy, Z, alpha=0.3)
axarr[idx].scatter(X_train[y_train==0, 0],X_train[y_train==0, 1],c=\'blue\', marker=\'^\')
axarr[idx].scatter(X_train[y_train==1, 0],X_train[y_train==1, 1],c=\'red\', marker=\'o\')
axarr[idx].set_title(tt)
axarr[0].set_ylabel(\'Alcohol\', fontsize=12)
plt.tight_layout()
plt.text(0, -0.2,s=\'OD280/OD315 of diluted wines\',ha=\'center\',va=\'center\',fontsize=12,transform=axarr[1].transAxes)
plt.show()
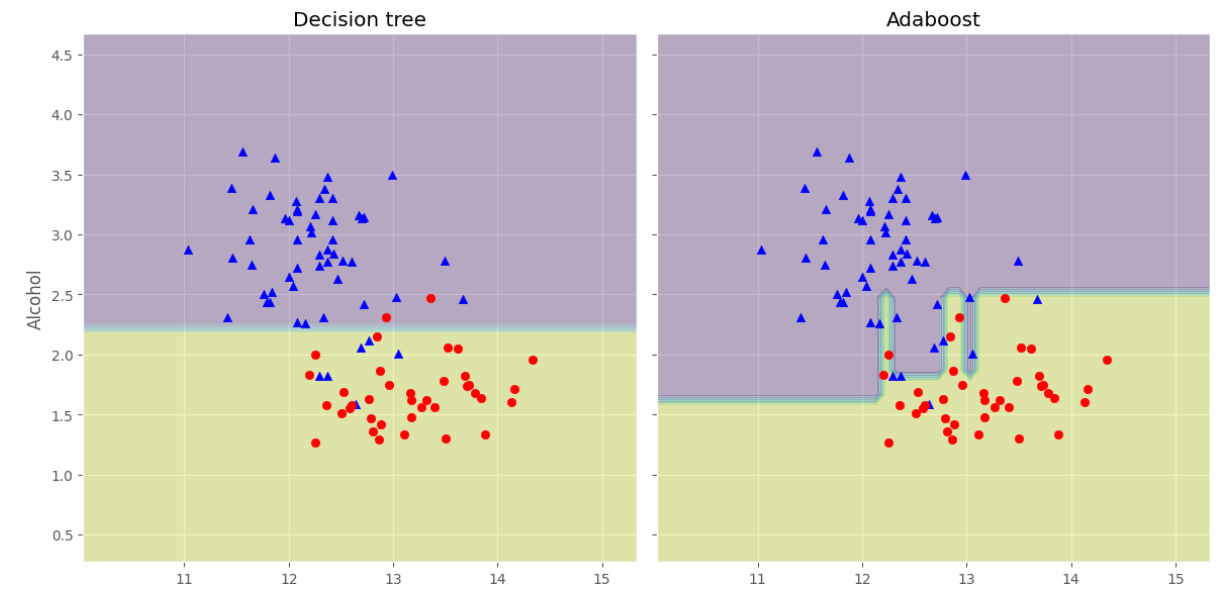
可以看淡AdaBoost的决策边界比单个决策树的决策边界复杂很多。
梯度提升GBDT
这里的理论解释用我对西瓜书的学习笔记吧:
GBDT是一种迭代的决策树算法,由多个决策树组成,所有树的结论累加起来作为最终答案。接下来从这两个方面进行介绍:Regression Decision Tree(回归树)、Gradient Boosting(梯度提升)、Shrinkage
DT
先补充一下决策树的类别,包含两种:
- 分类决策树:用于预测分类标签值,例如天气的类型、用户的性别等
- 回归决策树:用来预测连续实数值,例如天气温度、用户年龄
这两者的重要区别在于回归决策树的输出结果可以相加,分类决策树的输出结果不可以相加,例如回归决策树分别输出10岁、5岁、2岁,那他们相加得到17岁,可以作为结果使用;但是分类决策树分别输出男、男、女,这样的结果是无法进行相加处理的。因此GBDT中的树都是回归树,GBDT的核心在于累加所有树的结果作为最终结果。
回归树,救赎用树模型来做回归问题,其每一片叶子都输出一个预测值,而这个预测值一般是该片叶子所含训练集元素输出的均值,即$c_m=ave(y_i\\mid x_i \\in leaf_m)$
一般来说常见的回归决策树为CART,因此下面先介绍CART如何应用于回归问题。
在回归问题中,CART主要使用均方误差(mse)或者平均绝对误差(mae)来作为选择特征以及选择划分点时的依据。因此用于回归问题时,目标就是要构建出一个函数$f(x)$能够有效地拟合数据集$D$(样本数为n)中的元素,使得所选取的度量指标最小,例如取mse,即:
$$
min \\frac{1}{n} \\sum_{i=0}{n}(f(x_i)-y_i)2
$$
而对于构建好的CART回归树来说,假设其存在$M$片叶子,那么其mse的公式可以写成:
$$
min \\frac{1}{n}\\sum_{m=1}^{M}\\sum_{x_i \\in R_m}(c_m - y_i)^2
$$
其中$R_m$代表第$m$片叶子,而$c_m$代表第$m$片叶子的预测值。
要使得最小化mse,就需要对每一片叶子的mse都进行最小化。由统计学的知识可知道,只需要使**每片叶子的预测值为该片叶子中含有的训练元素的均值即可,即$c_m=ave(y_i\\mid x_i \\in leaf_m)$。
因此CART的学习方法就是遍历每一个变量且遍历变量中的每一个切分点,寻找能够使得mse最小的切分变量和切分点,即最小化如下公式:
$$
min_{j,s}[min_{c1}\\sum_{x_i\\in R_{1{j,s}}}(y_i-c_1)^2+min_{c_2}\\sum_{x_i\\in R_{2{j,s}}}(y_i-c_2)^2]
$$
另外一个值得了解的想法就是为什么CART必须是二叉树,其实是因为如果划分结点增多,即划分出来的区间也增多,遍历的难度加大。而如果想要细分为多个区域,实际上只需要让CART回归树的层次更深即可,这样遍历难度将小很多。
Gradient Boosting
梯度提升算法的流程与AdaBoost有点类似,而区别在于AdaBoost的特点在于每一轮是对分类正确和错误的样本分别进行修改权重,而梯度提升算法的每一轮学习都是为了减少上一轮的误差,具体可以看以下算法描述:
Step1、给定训练数据集T及损失函数L,这里可以认为损失函数为mse
Step2、初始化:
$$
f_0(x)=argmin_c\\sum_{i=1}{N}L(y_i,c)=argmin_c\\sum_{i=1}{N}(y_i - f_o(x_i))^2
$$
上式求解出来为:
$$
f_0(x)=\\sum_{i=1}^{N} \\frac{y_i}{N}=c
$$
Step3、目标基分类器(回归树)数目为$M$,对于$m=1,2,...M$:
(1)、对于$i=1,2,...N$,计算
$$
r_{mi}=-[\\frac{\\partial L(y_i,f(x_i)}{\\partial f(x_i)}]{f(x)=f{m-1}(x)}
$$
(2)、对$r_{mi}$进行拟合学习得到一个回归树,其叶结点区域为$R_{mj},j=1,2,...J$
(3)、对$j=1,2,...J$,计算该对应叶结点$R_{mj}$的输出预测值:
$$
c_{mj}=argmin_c\\sum_{x_i \\in R_{mj}}L(y_i,f_{m-1}(x_i)+c)
$$
(4)、更新$f_m(x)=f_{m-1}(x)+\\sum {j=1}^{J}c{mj}I(x \\in R_{mj})$
Step4、得到回归树:
$$
\\hat{f}(x)=f_M(x)=\\sum_{m=0}^{M} \\sum_{j=1}^{J}c_{mj}I(x\\in R_{mj})
$$
为什么损失函数的负梯度能够作为回归问题残差的近似值呢?:因为对于损失函数为mse来说,其求导的结果其实就是预测值与真实值之间的差值,那么负梯度也就是我们预测的残差$(y_i - f(x_i))$,因此只要下一个回归树对负梯度进行拟合再对多个回归树进行累加,就可以更好地逼近真实值。
Shrinkage
Shrinkage是一种用来对GBDT进行优化,防止其陷入过拟合的方法,其具体思想是:减少每一次迭代对于残差的收敛程度或者逼近程度,也就是说该思想认为迭代时每一次少逼近一些,然后迭代次数多一些的效果,比每一次多逼近一些,然后迭代次数少一些的效果要更好。那么具体的实现就是在每个回归树的累加前乘上学习率,即:
$$
f_m(x)=f_{m-1}(x)+\\gamma\\sum_{j=1}^{J}c_{mj}I(x\\in R_{mj})
$$
建模实现
下面对GBDT的模型进行解释以及建模实现。
引入相关库:
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor
GBDT还有一个做分类的模型是GradientBoostingClassifier。
下面整理一下模型的各个参数:
| 参数名称 | 参数意义 |
|---|---|
| loss | {‘ls’, ‘lad’, ‘huber’, ‘quantile’}, default=’ls’:‘ls’ 指最小二乘回归. ‘lad’是最小绝对偏差,是仅基于输入变量的顺序信息的高度鲁棒的损失函数;‘huber’ 是两者的结合 |
| quantile | 允许分位数回归(用于alpha指定分位数) |
| learning_rate | 学习率缩小了每棵树的贡献learning_rate。在learning_rate和n_estimators之间需要权衡。 |
| n_estimators | 要执行的提升次数,可以认为是基分类器的数目 |
| subsample | 用于拟合各个基础学习者的样本比例。如果小于1.0,则将导致随机梯度增强 |
| criterion | {\'friedman_mse\',\'mse\',\'mae\'},默认=\'friedman_mse\':“ mse”是均方误差,“ mae”是平均绝对误差。默认值“ friedman_mse”通常是最好的,因为在某些情况下它可以提供更好的近似值。 |
| min_samples_split | 拆分内部节点所需的最少样本数 |
| min_samples_leaf | 在叶节点处需要的最小样本数 |
| min_weight_fraction_leaf | 在所有叶节点处(所有输入样本)的权重总和中的最小加权分数。如果未提供sample_weight,则样本的权重相等。 |
| max_depth | 各个回归模型的最大深度。最大深度限制了树中节点的数量。调整此参数以获得最佳性能;最佳值取决于输入变量的相互作用 |
| min_impurity_decrease | 如果节点分裂会导致杂质(损失函数)的减少大于或等于该值,则该节点将被分裂 |
| min_impurity_split | 提前停止树木生长的阈值。如果节点的杂质高于阈值,则该节点将分裂 |
| max_features | {‘auto’, ‘sqrt’, ‘log2’},int或float:寻找最佳分割时要考虑的功能数量 |
可能各个参数一开始难以理解,但是随着使用会加深印象的。
X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
X_train, X_test = X[:200], X[200:]
y_train, y_test = y[:200], y[200:]
est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
max_depth=1, random_state=0, loss=\'ls\').fit(X_train, y_train)
mean_squared_error(y_test, est.predict(X_test))
5.009154859960321
from sklearn.datasets import make_regression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split
X, y = make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(
X, y, random_state=0)
reg = GradientBoostingRegressor(random_state=0)
reg.fit(X_train, y_train)
reg.score(X_test, y_test)
XGBoost
关于XGBoost的理论,其实它跟GBDT差不多,只不过在泰勒展开时考虑了二阶导函数,并在库实现中增加了很多的优化。而关于其参数的设置也相当复杂,因此这里简单介绍其用法即可。
安装XGBoost
pip install xgboost
数据接口
xgboost库所使用的数据类型为特殊的DMatrix类型,因此其读入文件比较特殊:
# 1.LibSVM文本格式文件
dtrain = xgb.DMatrix(\'train.svm.txt\')
dtest = xgb.DMatrix(\'test.svm.buffer\')
# 2.CSV文件(不能含类别文本变量,如果存在文本变量请做特征处理如one-hot)
dtrain = xgb.DMatrix(\'train.csv?format=csv&label_column=0\')
dtest = xgb.DMatrix(\'test.csv?format=csv&label_column=0\')
# 3.NumPy数组
data = np.random.rand(5, 10) # 5 entities, each contains 10 features
label = np.random.randint(2, size=5) # binary target
dtrain = xgb.DMatrix(data, label=label)
# 4.scipy.sparse数组
csr = scipy.sparse.csr_matrix((dat, (row, col)))
dtrain = xgb.DMatrix(csr)
# pandas数据框dataframe
data = pandas.DataFrame(np.arange(12).reshape((4,3)), columns=[\'a\', \'b\', \'c\'])
label = pandas.DataFrame(np.random.randint(2, size=4))
dtrain = xgb.DMatrix(data, label=label)
第一次读入后可以先保存为对应的二进制文件方便下次读取:
# 1.保存DMatrix到XGBoost二进制文件中
dtrain = xgb.DMatrix(\'train.svm.txt\')
dtrain.save_binary(\'train.buffer\')
# 2. 缺少的值可以用DMatrix构造函数中的默认值替换:
dtrain = xgb.DMatrix(data, label=label, missing=-999.0)
# 3.可以在需要时设置权重:
w = np.random.rand(5, 1)
dtrain = xgb.DMatrix(data, label=label, missing=-999.0, weight=w)
参数设置
import pandas as pd
df_wine = pd.read_csv(\'https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data\',header=None)
df_wine.columns = [\'Class label\', \'Alcohol\',\'Malic acid\', \'Ash\',\'Alcalinity of ash\',\'Magnesium\', \'Total phenols\',
\'Flavanoids\', \'Nonflavanoid phenols\',\'Proanthocyanins\',\'Color intensity\', \'Hue\',\'OD280/OD315 of diluted wines\',\'Proline\']
df_wine = df_wine[df_wine[\'Class label\'] != 1] # drop 1 class
y = df_wine[\'Class label\'].values
X = df_wine[[\'Alcohol\',\'OD280/OD315 of diluted wines\']].values
from sklearn.model_selection import train_test_split # 切分训练集与测试集
from sklearn.preprocessing import LabelEncoder # 标签化分类变量
import xgboost as xgb
le = LabelEncoder()
y = le.fit_transform(y)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,
random_state=1,stratify=y)
# 构造成目标类型的数据
dtrain = xgb.DMatrix(X_train, label = y_train)
dtest = xgb.DMatrix(X_test)
# booster参数
params = {
\"booster\": \'gbtree\', # 基分类器
\"objective\": \"multi:softmax\", # 使用softmax
\"num_class\": 10, # 类别数
\"gamma\":0.1, # 用于控制损失函数大于gamma时就剪枝
\"max_depth\": 12, # 构造树的深度,越大越容易过拟合
\"lambda\": 2, # 用来控制正则化参数
\"subsample\": 0.7, # 随机采样70%作为训练样本
\"colsample_bytree\": 0.7, # 生成树时进行列采样,相当于随机子空间
\"min_child_weight\":3,
\'verbosity\':0, # 设置成1则没有运行信息输出,设置成0则有,原文中这里的silent已经在新版本中不使用了
\"eta\": 0.007, # 相当于学习率
\"seed\": 1000, # 随机数种子
\"nthread\":4, # 线程数
\"eval_metric\": \"auc\"
}
plst = list(params.items()) # 这里必须加上list才能够使用后续的copy
这里如果发现报错为:
Parameters: { \"silent\" } are not used.
那是因为参数设置中新版本已经取消了silent参数,将其更改为verbosity即可。
如果在后续中发现:
\'dict_items\' object has no attribute \'copy\'
那是因为我们没有将items的返回变成list,像我上面那么改即可。
训练及预测
num_round = 10
bst = xgb.train(plst, dtrain ,num_round)
# 可以加上early_stoppint_rounds = 10来设置早停机制
# 如果要指定验证集,就是
# evallist = [(deval,\'eval\'),(dtrain, \'train\')]
# bst = xgb.train(plst, dtrain, num_round, evallist)
ypred = bst.predict(dtest) # 进行预测,跟sklearn的模型一致
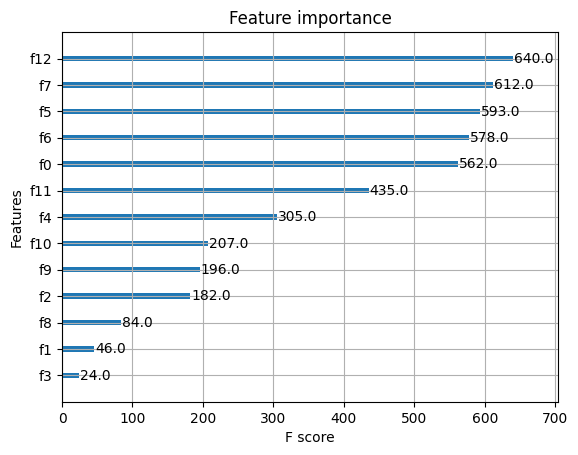
xgb.plot_importance(bst) # 绘制特征重要性的图
<AxesSubplot:title={\'center\':\'Feature importance\'}, xlabel=\'F score\', ylabel=\'Features\'>
模型保存与加载
bst.save_model(\"model_new_1121.model\")
bst.dump_model(\"dump.raw.txt\")
bst_new = xgb.Booster({\'nthread\':4}) # 先初始化参数
bst_new.load_model(\"model_new_1121.model\")
简单算例
分类案例
from sklearn.datasets import load_iris
import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score # 准确率
# 加载样本数据集
iris = load_iris()
X,y = iris.data,iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=1234565) # 数据集分割
# 算法参数
params = {
\'booster\': \'gbtree\',
\'objective\': \'multi:softmax\',
\'num_class\': 3,
\'gamma\': 0.1,
\'max_depth\': 6,
\'lambda\': 2,
\'subsample\': 0.7,
\'colsample_bytree\': 0.75,
\'min_child_weight\': 3,
\'verbosity\': 0,
\'eta\': 0.1,
\'seed\': 1,
\'nthread\': 4,
}
plst = list(params.items())
dtrain = xgb.DMatrix(X_train, y_train) # 生成数据集格式
num_rounds = 500
model = xgb.train(plst, dtrain, num_rounds) # xgboost模型训练
# 对测试集进行预测
dtest = xgb.DMatrix(X_test)
y_pred = model.predict(dtest)
# 计算准确率
accuracy = accuracy_score(y_test,y_pred)
print(\"accuarcy: %.2f%%\" % (accuracy*100.0))
# 显示重要特征
plot_importance(model)
plt.show()
accuarcy: 96.67%
回归案例
import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error
# 加载数据集
boston = load_boston()
X,y = boston.data,boston.target
# XGBoost训练过程
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
params = {
\'booster\': \'gbtree\',
\'objective\': \'reg:squarederror\', # 设置为回归,采用平方误差
\'gamma\': 0.1,
\'max_depth\': 5,
\'lambda\': 3,
\'subsample\': 0.7,
\'colsample_bytree\': 0.7,
\'min_child_weight\': 3,
\'verbosity\': 1,
\'eta\': 0.1,
\'seed\': 1000,
\'nthread\': 4,
}
dtrain = xgb.DMatrix(X_train, y_train)
num_rounds = 300
plst = list(params.items())
model = xgb.train(plst, dtrain, num_rounds)
# 对测试集进行预测
dtest = xgb.DMatrix(X_test)
ans = model.predict(dtest)
# 显示重要特征
plot_importance(model)
plt.show()
XGBoost的调参
该模型的调参一般步骤为:
- 确定学习速率和提升参数调优的初始值
- max_depth 和 min_child_weight 参数调优
- gamma参数调优
- subsample 和 colsample_bytree 参数优
- 正则化参数alpha调优
- 降低学习速率和使用更多的决策树
可以使用网格搜索来进行调优:
import xgboost as xgb
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import roc_auc_score
iris = load_iris()
X,y = iris.data,iris.target
col = iris.target_names
train_x, valid_x, train_y, valid_y = train_test_split(X, y, test_size=0.3, random_state=1) # 分训练集和验证集
parameters = {
\'max_depth\': [5, 10, 15, 20, 25],
\'learning_rate\': [0.01, 0.02, 0.05, 0.1, 0.15],
\'n_estimators\': [500, 1000, 2000, 3000, 5000],
\'min_child_weight\': [0, 2, 5, 10, 20],
\'max_delta_step\': [0, 0.2, 0.6, 1, 2],
\'subsample\': [0.6, 0.7, 0.8, 0.85, 0.95],
\'colsample_bytree\': [0.5, 0.6, 0.7, 0.8, 0.9],
\'reg_alpha\': [0, 0.25, 0.5, 0.75, 1],
\'reg_lambda\': [0.2, 0.4, 0.6, 0.8, 1],
\'scale_pos_weight\': [0.2, 0.4, 0.6, 0.8, 1]
}
xlf = xgb.XGBClassifier(max_depth=10,
learning_rate=0.01,
n_estimators=2000,
silent=True,
objective=\'multi:softmax\',
num_class=3 ,
nthread=-1,
gamma=0,
min_child_weight=1,
max_delta_step=0,
subsample=0.85,
colsample_bytree=0.7,
colsample_bylevel=1,
reg_alpha=0,
reg_lambda=1,
scale_pos_weight=1,
seed=0,
missing=None)
# 需要先给模型一定的初始值
gs = GridSearchCV(xlf, param_grid=parameters, scoring=\'accuracy\', cv=3)
gs.fit(train_x, train_y)
print(\"Best score: %0.3f\" % gs.best_score_)
print(\"Best parameters set: %s\" % gs.best_params_ )
Best score: 0.933
Best parameters set: {\'max_depth\': 5}
LightGBM算法
LightGBM也是像XGBoost一样,是一类集成算法,他跟XGBoost总体来说是一样的,算法本质上与Xgboost没有出入,只是在XGBoost的基础上进行了优化。
其调优过程也是一个很复杂的学问。这里就附上课程调优代码吧:
import lightgbm as lgb
from sklearn import metrics
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
canceData=load_breast_cancer()
X=canceData.data
y=canceData.target
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0,test_size=0.2)
### 数据转换
print(\'数据转换\')
lgb_train = lgb.Dataset(X_train, y_train, free_raw_data=False)
lgb_eval = lgb.Dataset(X_test, y_test, reference=lgb_train,free_raw_data=False)
### 设置初始参数--不含交叉验证参数
print(\'设置参数\')
params = {
\'boosting_type\': \'gbdt\',
\'objective\': \'binary\',
\'metric\': \'auc\',
\'nthread\':4,
\'learning_rate\':0.1
}
### 交叉验证(调参)
print(\'交叉验证\')
max_auc = float(\'0\')
best_params = {}
# 准确率
print(\"调参1:提高准确率\")
for num_leaves in range(5,100,5):
for max_depth in range(3,8,1):
params[\'num_leaves\'] = num_leaves
params[\'max_depth\'] = max_depth
cv_results = lgb.cv(
params,
lgb_train,
seed=1,
nfold=5,
metrics=[\'auc\'],
early_stopping_rounds=10,
verbose_eval=True
)
mean_auc = pd.Series(cv_results[\'auc-mean\']).max()
boost_rounds = pd.Series(cv_results[\'auc-mean\']).idxmax()
if mean_auc >= max_auc:
max_auc = mean_auc
best_params[\'num_leaves\'] = num_leaves
best_params[\'max_depth\'] = max_depth
if \'num_leaves\' and \'max_depth\' in best_params.keys():
params[\'num_leaves\'] = best_params[\'num_leaves\']
params[\'max_depth\'] = best_params[\'max_depth\']
# 过拟合
print(\"调参2:降低过拟合\")
for max_bin in range(5,256,10):
for min_data_in_leaf in range(1,102,10):
params[\'max_bin\'] = max_bin
params[\'min_data_in_leaf\'] = min_data_in_leaf
cv_results = lgb.cv(
params,
lgb_train,
seed=1,
nfold=5,
metrics=[\'auc\'],
early_stopping_rounds=10,
verbose_eval=True
)
mean_auc = pd.Series(cv_results[\'auc-mean\']).max()
boost_rounds = pd.Series(cv_results[\'auc-mean\']).idxmax()
if mean_auc >= max_auc:
max_auc = mean_auc
best_params[\'max_bin\']= max_bin
best_params[\'min_data_in_leaf\'] = min_data_in_leaf
if \'max_bin\' and \'min_data_in_leaf\' in best_params.keys():
params[\'min_data_in_leaf\'] = best_params[\'min_data_in_leaf\']
params[\'max_bin\'] = best_params[\'max_bin\']
print(\"调参3:降低过拟合\")
for feature_fraction in [0.6,0.7,0.8,0.9,1.0]:
for bagging_fraction in [0.6,0.7,0.8,0.9,1.0]:
for bagging_freq in range(0,50,5):
params[\'feature_fraction\'] = feature_fraction
params[\'bagging_fraction\'] = bagging_fraction
params[\'bagging_freq\'] = bagging_freq
cv_results = lgb.cv(
params,
lgb_train,
seed=1,
nfold=5,
metrics=[\'auc\'],
early_stopping_rounds=10,
verbose_eval=True
)
mean_auc = pd.Series(cv_results[\'auc-mean\']).max()
boost_rounds = pd.Series(cv_results[\'auc-mean\']).idxmax()
if mean_auc >= max_auc:
max_auc=mean_auc
best_params[\'feature_fraction\'] = feature_fraction
best_params[\'bagging_fraction\'] = bagging_fraction
best_params[\'bagging_freq\'] = bagging_freq
if \'feature_fraction\' and \'bagging_fraction\' and \'bagging_freq\' in best_params.keys():
params[\'feature_fraction\'] = best_params[\'feature_fraction\']
params[\'bagging_fraction\'] = best_params[\'bagging_fraction\']
params[\'bagging_freq\'] = best_params[\'bagging_freq\']
print(\"调参4:降低过拟合\")
for lambda_l1 in [1e-5,1e-3,1e-1,0.0,0.1,0.3,0.5,0.7,0.9,1.0]:
for lambda_l2 in [1e-5,1e-3,1e-1,0.0,0.1,0.4,0.6,0.7,0.9,1.0]:
params[\'lambda_l1\'] = lambda_l1
params[\'lambda_l2\'] = lambda_l2
cv_results = lgb.cv(
params,
lgb_train,
seed=1,
nfold=5,
metrics=[\'auc\'],
early_stopping_rounds=10,
verbose_eval=True
)
mean_auc = pd.Series(cv_results[\'auc-mean\']).max()
boost_rounds = pd.Series(cv_results[\'auc-mean\']).idxmax()
if mean_auc >= max_auc:
max_auc=mean_auc
best_params[\'lambda_l1\'] = lambda_l1
best_params[\'lambda_l2\'] = lambda_l2
if \'lambda_l1\' and \'lambda_l2\' in best_params.keys():
params[\'lambda_l1\'] = best_params[\'lambda_l1\']
params[\'lambda_l2\'] = best_params[\'lambda_l2\']
print(\"调参5:降低过拟合2\")
for min_split_gain in [0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0]:
params[\'min_split_gain\'] = min_split_gain
cv_results = lgb.cv(
params,
lgb_train,
seed=1,
nfold=5,
metrics=[\'auc\'],
early_stopping_rounds=10,
verbose_eval=True
)
mean_auc = pd.Series(cv_results[\'auc-mean\']).max()
boost_rounds = pd.Series(cv_results[\'auc-mean\']).idxmax()
if mean_auc >= max_auc:
max_auc=mean_auc
best_params[\'min_split_gain\'] = min_split_gain
if \'min_split_gain\' in best_params.keys():
params[\'min_split_gain\'] = best_params[\'min_split_gain\']
print(best_params)
{\'bagging_fraction\': 0.7,
\'bagging_freq\': 30,
\'feature_fraction\': 0.8,
\'lambda_l1\': 0.1,
\'lambda_l2\': 0.0,
\'max_bin\': 255,
\'max_depth\': 4,
\'min_data_in_leaf\': 81,
\'min_split_gain\': 0.1,
\'num_leaves\': 10}
Blending与Stacking
Stacking,这个集成方法在比赛中被称为“懒人”算法,因为它不需要花费过多时间的调参就可以得到一个效果不错的算法。
Stacking集成算法可以理解为一个两层的集成,第一层含有多个基础分类器,把预测的结果(元特征)提供给第二层, 而第二层的分类器通常是逻辑回归,他把一层分类器的结果当做特征做拟合输出预测结果。
而Blending就是简化版的Stacking,因此我们先对前者进行介绍。
Blending集成学习算法
算法流程
Blending的算法流程为:
- 将数据集划分为训练集与测试集,训练集再划分为训练集与验证集
- 创建第一层的多个模型(可同质也可异质),然后对训练集进行学习
- 第一层的模型训练完成后对验证集和测试集做出预测,假设K个模型,那么就得到$A_1,...,A_K$和$B_1,...,B_K$,其中每个代表一个基分类器对验证集或测试集的所有结果输出。
- 创建第二层的分类器,其将$A_1,...,A_K$作为训练数据集,那么样本数目就是验证集的样本数目,特征数目就是K,将真实的验证集标签作为标签,从而来训练该分类器
- 对测试集的预测则是将$B_1,...,B_K$作为特征,用第二层的分类器进行预测。
具体实现
具体的实现如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use(\"ggplot\")
%matplotlib inline
import seaborn as sns
# 创建数据
from sklearn import datasets
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
data, target = make_blobs(n_samples=10000, centers=2, random_state=1, cluster_std=1.0 )
## 创建训练集和测试集
X_train1,X_test,y_train1,y_test = train_test_split(data, target, test_size=0.2, random_state=1)
## 创建训练集和验证集
X_train,X_val,y_train,y_val = train_test_split(X_train1, y_train1, test_size=0.3, random_state=1)
print(\"The shape of training X:\",X_train.shape)
print(\"The shape of training y:\",y_train.shape)
print(\"The shape of test X:\",X_test.shape)
print(\"The shape of test y:\",y_test.shape)
print(\"The shape of validation X:\",X_val.shape)
print(\"The shape of validation y:\",y_val.shape)
The shape of training X: (5600, 2)
The shape of training y: (5600,)
The shape of test X: (2000, 2)
The shape of test y: (2000,)
The shape of validation X: (2400, 2)
The shape of validation y: (2400,)
# 设置第一层分类器
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
clfs = [SVC(probability = True),RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion=\'gini\'),KNeighborsClassifier()]
# 设置第二层分类器
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# 输出第一层的验证集结果与测试集结果
val_features = np.zeros((X_val.shape[0],len(clfs))) # 初始化验证集结果
test_features = np.zeros((X_test.shape[0],len(clfs))) # 初始化测试集结果
for i,clf in enumerate(clfs):
clf.fit(X_train,y_train)
# porba函数得到的是对于每个类别的预测分数,取出第一列代表每个样本为第一类的概率
val_feature = clf.predict_proba(X_val)[:, 1]
test_feature = clf.predict_proba(X_test)[:,1]
val_features[:,i] = val_feature
test_features[:,i] = test_feature
# 将第一层的验证集的结果输入第二层训练第二层分类器
lr.fit(val_features,y_val)
# 输出预测的结果
from sklearn.model_selection import cross_val_score
cross_val_score(lr,test_features,y_test,cv=5)
array([1., 1., 1., 1., 1.])
可以看到交叉验证的结果很好。
对于小作业我总有些疑问,那就是这个iris数据的特征为4,然后预测类别数为3,那么首先是特征为4超过3维度,应该怎么决策边界,难道舍弃一些维度吗?其次是类别数为3,那么在计算的时候取的是[;1]也就是类别为1的概率,那么只取这个作为下一层的特征是否足够,因为类别为0和类别为2的概率完全舍弃的话不行吧。
Stacking
算法流程
下面这张图可以很好的理解流程:
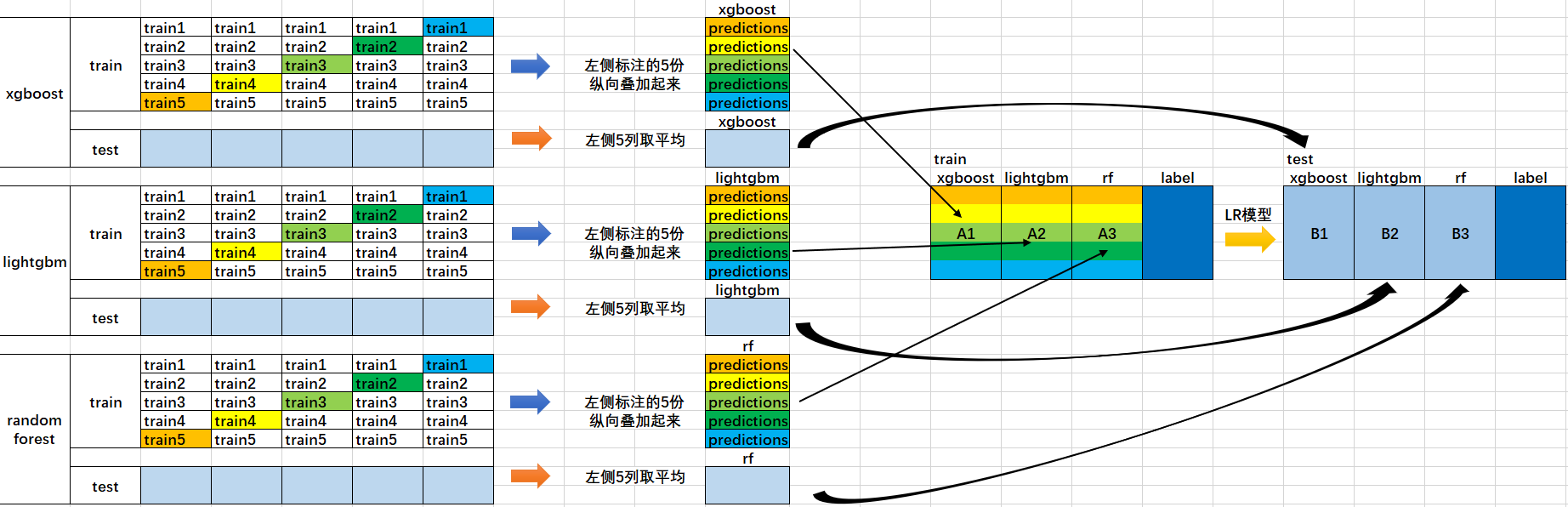
- 首先将所有数据划分测试集和训练集,假设训练集总共有10000行,测试集总共2500行,对第一层的分类器进行5折交叉验证,那么验证集就划分为2000行,训练集为8000行。
- 每次验证就相当于使用8000条训练数据去训练模型然后用2000条验证数据去验证,并且每一次都将训练出来的模型对测试集的2500条数据进行预测,那么经过5次交叉验证,对于每个基分类器可以得到中间的$5\\times 2000$的五份验证集数据,以及$5\\times 2500$的五份测试集的预测结果
- 接下来将验证集拼成10000行长的矩阵,记为$A_1$(对于第1个基分类器),而对于$5\\times 2500$行的测试集的预测结果进行加权平均,得到2500行1列的矩阵,记为$B_1$
- 那么假设这里是3个基分类器,因此有$A_1,A_2,A_3,B_1,B_2,B_3$六个矩阵,接下来将$A_1,A_2,A_3$矩阵拼成10000行3列的矩阵作为训练数据集,而验证集的真实标签作为训练数据的标签;将$B_1,B_2,B_3$拼成2500行3列的矩阵作为测试数据集合。
- 那么对下层的学习器进行训练
具体代码
from sklearn import datasets
iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target # 只取出两个特征
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier
RANDOM_SEED = 42
clf1 = KNeighborsClassifier(n_neighbors = 1)
clf2 = RandomForestClassifier(random_state = RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers = [clf1, clf2, clf3], # 第一层的分类器
meta_classifier = lr, # 第二层的分类器
random_state = RANDOM_SEED)
print(\"3折交叉验证:\\n\")
for clf, label in zip([clf1, clf2, clf3, sclf], [\'KNN\',\'RandomForest\',\'Naive Bayes\',
\'Stack\']):
scores = cross_val_score(clf, X, y, cv = 3, scoring = \'accuracy\')
print(\"Accuracy: %0.2f (+/- %0.2f) [%s]\" % (scores.mean(), scores.std(), label))
3折交叉验证:
Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [RandomForest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.93 (+/- 0.02) [Stack]
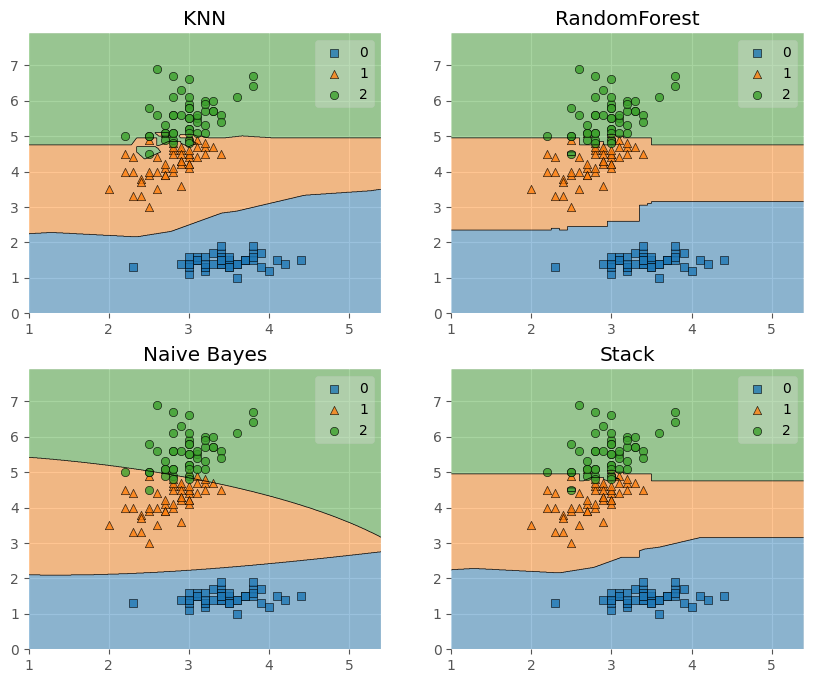
接下来尝试将决策边界画出:
from mlxtend.plotting import plot_decision_regions
import matplotlib.gridspec as gridspec
import itertools
gs = gridspec.GridSpec(2,2)
# 可以理解为将子图划分为了2*2的区域
fig = plt.figure(figsize = (10,8))
for clf, lab, grd in zip([clf1, clf2, clf3, sclf], [\'KNN\',
\'RandomForest\',
\'Naive Bayes\',
\'Stack\'],
itertools.product([0,1],repeat=2)):
clf.fit(X, y)
ax = plt.subplot(gs[grd[0],grd[1]])
# grd依次为(0,0),(0,1),(1,0),(1,1),那么传入到gs中就可以得到指定的区域
fig = plot_decision_regions(X = X, y = y, clf = clf)
plt.title(lab)
plt.show()
这里补充两个第一次见到的函数:
-
itertools.product([0,1],repeat = 2):该模块下的product函数一般是传进入两个集合,例如传进入[0,1],[1,2]然后返回[(0,1),(0,2),(1,1),(1,2)],那么这里只传进去一个参数然后repeat=2相当于传进去[0,1],[0,1],产生[(0,0),(0,1),(1,0),(1,1)],如果repeat=3就是
(0, 0, 0) (0, 0, 1) (0, 1, 0) (0, 1, 1) (1, 0, 0) (1, 0, 1) (1, 1, 0) (1, 1, 1) -
gs = gridspec.GridSpec(2,2):这个函数相当于我将子图划分为2*2总共4个区域,那么在下面subplot中就可以例如调用gs[0,1]来获取(0,1)这个区域,下面的例子或者更好理解:
plt.figure() gs=gridspec.GridSpec(3,3)#分为3行3列 ax1=plt.subplot(gs[0,:]) ax1=plt.subplot(gs[1,:2]) ax1=plt.subplot(gs[1:,2]) ax1=plt.subplot(gs[-1,0]) ax1=plt.subplot(gs[-1,-2])
继续回到Stacking中。
前面我们是使用第一层的分类器其输出作为第二层的输入,那么如果希望使用第一层所有基分类器所产生的的类别概率值作为第二层分类器的数目,需要在StackingClassifier 中增加一个参数设置:use_probas = True。还有一个参数设置average_probas = True,那么这些基分类器所产出的概率值将按照列被平均,否则会拼接

我们来进行尝试:
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
use_probas=True, # 使用概率
meta_classifier=lr,
random_state=42)
print(\'3折交叉验证:\')
for clf, label in zip([clf1, clf2, clf3, sclf],
[\'KNN\',
\'Random Forest\',
\'Naive Bayes\',
\'StackingClassifier\']):
scores = cross_val_score(clf, X, y, cv=3, scoring=\'accuracy\')
print(\"Accuracy: %0.2f (+/- %0.2f) [%s]\"
% (scores.mean(), scores.std(), label))
3折交叉验证:
Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [Random Forest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.95 (+/- 0.02) [StackingClassifier]
另外,还可以跟网格搜索相结合:
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from mlxtend.classifier import StackingCVClassifier
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
meta_classifier=lr,
random_state=42)
params = {\'kneighborsclassifier__n_neighbors\': [1, 5],
\'randomforestclassifier__n_estimators\': [10, 50],
\'meta_classifier__C\': [0.1, 10.0]}#
grid = GridSearchCV(estimator=sclf, # 分类为stacking
param_grid=params, # 设置的参数
cv=5,
refit=True)
#最后一个参数代表在搜索参数结束后,用最佳参数结果再次fit一遍全部数据集
grid.fit(X, y)
cv_keys = (\'mean_test_score\', \'std_test_score\', \'params\')
for r,_ in enumerate(grid.cv_results_[\'mean_test_score\']):
print(\"%0.3f +/- %0.2f %r\"
% (grid.cv_results_[cv_keys[0]][r],
grid.cv_results_[cv_keys[1]][r] / 2.0,
grid.cv_results_[cv_keys[2]][r]))
print(\'Best parameters: %s\' % grid.best_params_)
print(\'Accuracy: %.2f\' % grid.best_score_)
0.947 +/- 0.03 {\'kneighborsclassifier__n_neighbors\': 1, \'meta_classifier__C\': 0.1, \'randomforestclassifier__n_estimators\': 10}
0.933 +/- 0.02 {\'kneighborsclassifier__n_neighbors\': 1, \'meta_classifier__C\': 0.1, \'randomforestclassifier__n_estimators\': 50}
0.940 +/- 0.02 {\'kneighborsclassifier__n_neighbors\': 1, \'meta_classifier__C\': 10.0, \'randomforestclassifier__n_estimators\': 10}
0.940 +/- 0.02 {\'kneighborsclassifier__n_neighbors\': 1, \'meta_classifier__C\': 10.0, \'randomforestclassifier__n_estimators\': 50}
0.953 +/- 0.02 {\'kneighborsclassifier__n_neighbors\': 5, \'meta_classifier__C\': 0.1, \'randomforestclassifier__n_estimators\': 10}
0.953 +/- 0.02 {\'kneighborsclassifier__n_neighbors\': 5, \'meta_classifier__C\': 0.1, \'randomforestclassifier__n_estimators\': 50}
0.953 +/- 0.02 {\'kneighborsclassifier__n_neighbors\': 5, \'meta_classifier__C\': 10.0, \'randomforestclassifier__n_estimators\': 10}
0.953 +/- 0.02 {\'kneighborsclassifier__n_neighbors\': 5, \'meta_classifier__C\': 10.0, \'randomforestclassifier__n_estimators\': 50}
Best parameters: {\'kneighborsclassifier__n_neighbors\': 5, \'meta_classifier__C\': 0.1, \'randomforestclassifier__n_estimators\': 10}
Accuracy: 0.95
而如果希望在算法中多次使用某个模型,就可以在参数网格中添加一个附加的数字后缀:
params = {\'kneighborsclassifier-1__n_neighbors\': [1, 5],
\'kneighborsclassifier-2__n_neighbors\': [1, 5],
\'randomforestclassifier__n_estimators\': [10, 50],
\'meta_classifier__C\': [0.1, 10.0]}
我们还可以结合随机子空间的思想,为Stacking第一层的不同子模型设置不同的特征:
from sklearn.datasets import load_iris
from mlxtend.classifier import StackingCVClassifier
from mlxtend.feature_selection import ColumnSelector
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
iris = load_iris()
X = iris.data
y = iris.target
pipe1 = make_pipeline(ColumnSelector(cols=(0, 2)), # 选择第0,2列
LogisticRegression()) # 可以理解为先挑选特征再以基分类器为逻辑回归
pipe2 = make_pipeline(ColumnSelector(cols=(1, 2, 3)), # 选择第1,2,3列
LogisticRegression()) # 两个基分类器都是逻辑回归
sclf = StackingCVClassifier(classifiers=[pipe1, pipe2],
# 两个基分类器区别在于使用特征不同
meta_classifier=LogisticRegression(),
random_state=42)
sclf.fit(X, y)

下面我们可以画ROC曲线:
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
iris = datasets.load_iris()
X, y = iris.data[:, [0, 1]], iris.target # 只用了前两个特征
y = label_binarize(y, classes = [0,1,2])
# 因为y里面有三个类别,分类标注为0,1,2,这里是将y变换为一个n*3的矩阵
# 每一行为3代表类别数目为3,然后如果y是第0类就是100,第一类就是010,第二类就是001
# 关键在于后面的classes如何制定,如果是[0,2,1]那么是第二类就是010,第一类是001
n_classes = y.shape[1]
RANDOM_SEED = 42
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33,
random_state=RANDOM_SEED)
clf1 = LogisticRegression()
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = SVC(random_state=RANDOM_SEED)
lr = LogisticRegression()
sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
meta_classifier=lr)
classifier = OneVsRestClassifier(sclf)
# 这个对象在拟合时会对每一类学习一个分类器,用来做二分类,分别该类和其他所有类
y_score = classifier.fit(X_train, y_train).decision_function(X_test)
# decision_function是预测X_test在决策边界的哪一边,然后距离有多大,可以认为是评估指标
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr[\"micro\"], tpr[\"micro\"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc[\"micro\"] = auc(fpr[\"micro\"], tpr[\"micro\"])
plt.figure()
lw = 2
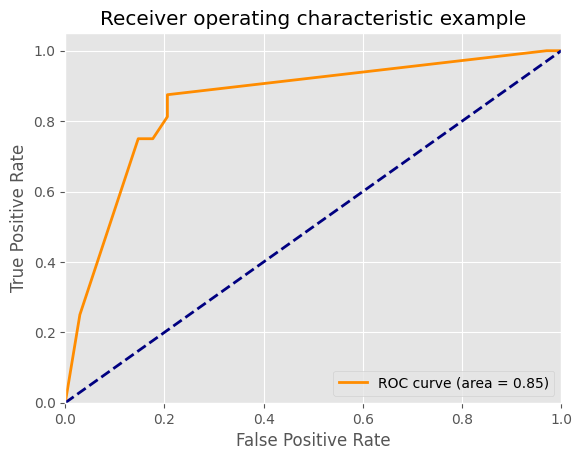
plt.plot(fpr[2], tpr[2], color=\'darkorange\',
lw=lw, label=\'ROC curve (area = %0.2f)\' % roc_auc[2])
plt.plot([0, 1], [0, 1], color=\'navy\', lw=lw, linestyle=\'--\')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel(\'False Positive Rate\')
plt.ylabel(\'True Positive Rate\')
plt.title(\'Receiver operating characteristic example\')
plt.legend(loc=\"lower right\")
plt.show()
集成学习案例1——幸福感预测
背景介绍
此案例是一个数据挖掘类型的比赛——幸福感预测的baseline。比赛的数据使用的是官方的《中国综合社会调查(CGSS)》文件中的调查结果中的数据,其共包含有139个维度的特征,包括个体变量(性别、年龄、地域、职业、健康、婚姻与政治面貌等等)、家庭变量(父母、配偶、子女、家庭资本等等)、社会态度(公平、信用、公共服务)等特征。赛题要求使用以上 139 维的特征,使用 8000 余组数据进行对于个人幸福感的预测(预测值为1,2,3,4,5,其中1代表幸福感最低,5代表幸福感最高)
具体代码
导入需要的包
import os
import time
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
from datetime import datetime
import matplotlib.pyplot as plt
from sklearn.metrics import roc_auc_score, roc_curve, mean_squared_error,mean_absolute_error, f1_score
import lightgbm as lgb
import xgboost as xgb
from sklearn.ensemble import RandomForestRegressor as rfr
from sklearn.ensemble import ExtraTreesRegressor as etr
from sklearn.linear_model import BayesianRidge as br
from sklearn.ensemble import GradientBoostingRegressor as gbr
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import LinearRegression as lr
from sklearn.linear_model import ElasticNet as en
from sklearn.kernel_ridge import KernelRidge as kr
from sklearn.model_selection import KFold, StratifiedKFold,GroupKFold, RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn import preprocessing
import logging
import warnings
warnings.filterwarnings(\'ignore\') #消除warning
导入数据集
train = pd.read_csv(\"train.csv\", parse_dates=[\'survey_time\'],encoding=\'latin-1\')
# 第二个参数代表把那一列转换为时间类型
test = pd.read_csv(\"test.csv\", parse_dates=[\'survey_time\'],encoding=\'latin-1\')
#latin-1向下兼容ASCII
train = train[train[\"happiness\"] != -8].reset_index(drop=True)
# =8代表没有回答是否幸福因此不要这些,reset_index是重置索引,因为行数变化了
train_data_copy = train.copy() # 完全删除掉-8的行
target_col = \"happiness\"
target = train_data_copy[target_col]
del train_data_copy[target_col]
data = pd.concat([train_data_copy, test], axis = 0, ignore_index = True)
# 把他们按照行叠在一起
数据预处理
数据中出现的主要负数值是-1,-2,-3,-8,因此分别定义函数可以处理。
#make feature +5
#csv中有复数值:-1、-2、-3、-8,将他们视为有问题的特征,但是不删去
def getres1(row):
return len([x for x in row.values if type(x)==int and x<0])
def getres2(row):
return len([x for x in row.values if type(x)==int and x==-8])
def getres3(row):
return len([x for x in row.values if type(x)==int and x==-1])
def getres4(row):
return len([x for x in row.values if type(x)==int and x==-2])
def getres5(row):
return len([x for x in row.values if type(x)==int and x==-3])
#检查数据
# 这里的意思就是将函数应用到表格中,而axis=1是应用到每一行,因此得到新的特征行数跟原来
# 是一样的,统计了该行为负数的个数
data[\'neg1\'] = data[data.columns].apply(lambda row:getres1(row),axis=1)
data.loc[data[\'neg1\']>20,\'neg1\'] = 20 #平滑处理
data[\'neg2\'] = data[data.columns].apply(lambda row:getres2(row),axis=1)
data[\'neg3\'] = data[data.columns].apply(lambda row:getres3(row),axis=1)
data[\'neg4\'] = data[data.columns].apply(lambda row:getres4(row),axis=1)
data[\'neg5\'] = data[data.columns].apply(lambda row:getres5(row),axis=1)
而对于缺失值的填补,需要针对特征加上自己的理解,例如如果家庭成员缺失值,那么就填补为1,例如家庭收入确实,那么可以填补为整个特征的平均值等等,这部分可以自己发挥想象力,采用fillna进行填补。
先查看哪些列存在缺失值需要填补:
data.isnull().sum()[data.isnull().sum() > 0]
edu_other 10950
edu_status 1569
edu_yr 2754
join_party 9831
property_other 10867
hukou_loc 4
social_neighbor 1096
social_friend 1096
work_status 6932
work_yr 6932
work_type 6931
work_manage 6931
family_income 1
invest_other 10911
minor_child 1447
marital_1st 1128
s_birth 2365
marital_now 2445
s_edu 2365
s_political 2365
s_hukou 2365
s_income 2365
s_work_exper 2365
s_work_status 7437
s_work_type 7437
dtype: int64
那么对以上这些特征进行处理:
data[\'work_status\'] = data[\'work_status\'].fillna(0)
data[\'work_yr\'] = data[\'work_yr\'].fillna(0)
data[\'work_manage\'] = data[\'work_manage\'].fillna(0)
data[\'work_type\'] = data[\'work_type\'].fillna(0)
data[\'edu_yr\'] = data[\'edu_yr\'].fillna(0)
data[\'edu_status\'] = data[\'edu_status\'].fillna(0)
data[\'s_work_type\'] = data[\'s_work_type\'].fillna(0)
data[\'s_work_status\'] = data[\'s_work_status\'].fillna(0)
data[\'s_political\'] = data[\'s_political\'].fillna(0)
data[\'s_hukou\'] = data[\'s_hukou\'].fillna(0)
data[\'s_income\'] = data[\'s_income\'].fillna(0)
data[\'s_birth\'] = data[\'s_birth\'].fillna(0)
data[\'s_edu\'] = data[\'s_edu\'].fillna(0)
data[\'s_work_exper\'] = data[\'s_work_exper\'].fillna(0)
data[\'minor_child\'] = data[\'minor_child\'].fillna(0)
data[\'marital_now\'] = data[\'marital_now\'].fillna(0)
data[\'marital_1st\'] = data[\'marital_1st\'].fillna(0)
data[\'social_neighbor\']=data[\'social_neighbor\'].fillna(0)
data[\'social_friend\']=data[\'social_friend\'].fillna(0)
data[\'hukou_loc\']=data[\'hukou_loc\'].fillna(1) #最少为1,表示户口
data[\'family_income\']=data[\'family_income\'].fillna(66365) #删除问题值后的平均值
特殊格式的信息也需要处理,例如跟时间有关的信息,可以化成对应方便处理的格式,以及对年龄进行分段处理:
data[\'survey_time\'] = pd.to_datetime(data[\'survey_time\'], format=\'%Y-%m-%d\',
errors=\'coerce\')
#防止时间格式不同的报错errors=\'coerce‘,格式不对就幅值NaN
data[\'survey_time\'] = data[\'survey_time\'].dt.year #仅仅是year,方便计算年龄
data[\'age\'] = data[\'survey_time\']-data[\'birth\']
bins = [0,17,26,34,50,63,100]
data[\'age_bin\'] = pd.cut(data[\'age\'], bins, labels=[0,1,2,3,4,5])
还有就是对一些异常值的处理,例如在某些问题中不应该出现负数但是出现了负数,那么就可以根据我们的直观理解来进行处理:
# 对宗教进行处理
data.loc[data[\'religion\'] < 0, \'religion\'] = 1 # 1代表不信仰宗教
data.loc[data[\'religion_freq\'] < 0, \"religion_freq\"] = 0 # 代表不参加
# 教育
data.loc[data[\'edu\'] < 0, \'edu\'] = 1 # 负数说明没有接受过任何教育
data.loc[data[\'edu_status\'] < 0 , \'edu_status\'] = 0
data.loc[data[\'edu_yr\']<0,\'edu_yr\'] = 0
# 收入
data.loc[data[\'income\']<0,\'income\'] = 0 #认为无收入
#对‘政治面貌’处理
data.loc[data[\'political\']<0,\'political\'] = 1 #认为是群众
#对体重处理
data.loc[(data[\'weight_jin\']<=80)&(data[\'height_cm\']>=160),\'weight_jin\']= data[\'weight_jin\']*2
data.loc[data[\'weight_jin\']<=60,\'weight_jin\']= data[\'weight_jin\']*2 #没有60斤的成年人吧
#对身高处理
data.loc[data[\'height_cm\']<130,\'height_cm\'] = 150 #成年人的实际情况
#对‘健康’处理
data.loc[data[\'health\']<0,\'health\'] = 4 #认为是比较健康
data.loc[data[\'health_problem\']<0,\'health_problem\'] = 4 # 4代表很少
#对‘沮丧’处理
data.loc[data[\'depression\']<0,\'depression\'] = 4 #很少
#对‘媒体’处理
data.loc[data[\'media_1\']<0,\'media_1\'] = 1 #都是从不
data.loc[data[\'media_2\']<0,\'media_2\'] = 1
data.loc[data[\'media_3\']<0,\'media_3\'] = 1
data.loc[data[\'media_4\']<0,\'media_4\'] = 1
data.loc[data[\'media_5\']<0,\'media_5\'] = 1
data.loc[data[\'media_6\']<0,\'media_6\'] = 1
#对‘空闲活动’处理
data.loc[data[\'leisure_1\']<0,\'leisure_1\'] = data[\'leisure_1\'].mode() # 众数
data.loc[data[\'leisure_2\']<0,\'leisure_2\'] = data[\'leisure_2\'].mode()
data.loc[data[\'leisure_3\']<0,\'leisure_3\'] = data[\'leisure_3\'].mode()
data.loc[data[\'leisure_4\']<0,\'leisure_4\'] = data[\'leisure_4\'].mode()
data.loc[data[\'leisure_5\']<0,\'leisure_5\'] = data[\'leisure_5\'].mode()
data.loc[data[\'leisure_6\']<0,\'leisure_6\'] = data[\'leisure_6\'].mode()
data.loc[data[\'leisure_7\']<0,\'leisure_7\'] = data[\'leisure_7\'].mode()
data.loc[data[\'leisure_8\']<0,\'leisure_8\'] = data[\'leisure_8\'].mode()
data.loc[data[\'leisure_9\']<0,\'leisure_9\'] = data[\'leisure_9\'].mode()
data.loc[data[\'leisure_10\']<0,\'leisure_10\'] = data[\'leisure_10\'].mode()
data.loc[data[\'leisure_11\']<0,\'leisure_11\'] = data[\'leisure_11\'].mode()
data.loc[data[\'leisure_12\']<0,\'leisure_12\'] = data[\'leisure_12\'].mode()
data.loc[data[\'socialize\']<0, \'socialize\'] = 2 # 社交,很少
data.loc[data[\'relax\']<0, \'relax\'] = 2 # 放松,很少
data.loc[data[\'learn\']<0, \'learn\'] = 2 # 学习,很少
data.loc[data[\'social_neighbor\']<0, \'social_neighbor\'] = 6 # 一年1次或更少社交
data.loc[data[\'social_friend\']<0, \'social_friend\'] = 6
data.loc[data[\'socia_outing\']<0, \'socia_outing\'] = 1
data.loc[data[\'neighbor_familiarity\']<0,\'social_neighbor\']= 2 # 不太熟悉
data.loc[data[\'equity\']<0,\'equity\'] = 3 # 不知道公不公平
#对‘社会等级’处理
data.loc[data[\'class_10_before\']<0,\'class_10_before\'] = 3
data.loc[data[\'class\']<0,\'class\'] = 5
data.loc[data[\'class_10_after\']<0,\'class_10_after\'] = 5
data.loc[data[\'class_14\']<0,\'class_14\'] = 2
#对‘工作情况’处理
data.loc[data[\'work_status\']<0,\'work_status\'] = 0
data.loc[data[\'work_yr\']<0,\'work_yr\'] = 0
data.loc[data[\'work_manage\']<0,\'work_manage\'] = 0
data.loc[data[\'work_type\']<0,\'work_type\'] = 0
#对‘社会保障’处理
data.loc[data[\'insur_1\']<0,\'insur_1\'] = 1
data.loc[data[\'insur_2\']<0,\'insur_2\'] = 1
data.loc[data[\'insur_3\']<0,\'insur_3\'] = 1
data.loc[data[\'insur_4\']<0,\'insur_4\'] = 1
data.loc[data[\'insur_1\']==0,\'insur_1\'] = 0
data.loc[data[\'insur_2\']==0,\'insur_2\'] = 0
data.loc[data[\'insur_3\']==0,\'insur_3\'] = 0
data.loc[data[\'insur_4\']==0,\'insur_4\'] = 0
#对家庭情况处理
family_income_mean = data[\'family_income\'].mean() # 计算均值
data.loc[data[\'family_income\']<0,\'family_income\'] = family_income_mean
data.loc[data[\'family_m\']<0,\'family_m\'] = 2
data.loc[data[\'family_status\']<0,\'family_status\'] = 3
data.loc[data[\'house\']<0,\'house\'] = 1
data.loc[data[\'car\']<0,\'car\'] = 0
data.loc[data[\'car\']==2,\'car\'] = 0 #变为0和1
data.loc[data[\'son\']<0,\'son\'] = 0
data.loc[data[\'daughter\']<0,\'daughter\'] = 0
data.loc[data[\'minor_child\']<0,\'minor_child\'] = 0
#对‘婚姻’处理
data.loc[data[\'marital_1st\']<0,\'marital_1st\'] = 0
data.loc[data[\'marital_now\']<0,\'marital_now\'] = 0
#对‘配偶’处理
data.loc[data[\'s_birth\']<0,\'s_birth\'] = 0
data.loc[data[\'s_edu\']<0,\'s_edu\'] = 0
data.loc[data[\'s_political\']<0,\'s_political\'] = 0
data.loc[data[\'s_hukou\']<0,\'s_hukou\'] = 0
data.loc[data[\'s_income\']<0,\'s_income\'] = 0
data.loc[data[\'s_work_type\']<0,\'s_work_type\'] = 0
data.loc[data[\'s_work_status\']<0,\'s_work_status\'] = 0
data.loc[data[\'s_work_exper\']<0,\'s_work_exper\'] = 0
#对‘父母情况’处理
data.loc[data[\'f_birth\']<0,\'f_birth\'] = 1945
data.loc[data[\'f_edu\']<0,\'f_edu\'] = 1
data.loc[data[\'f_political\']<0,\'f_political\'] = 1
data.loc[data[\'f_work_14\']<0,\'f_work_14\'] = 2
data.loc[data[\'m_birth\']<0,\'m_birth\'] = 1940
data.loc[data[\'m_edu\']<0,\'m_edu\'] = 1
data.loc[data[\'m_political\']<0,\'m_political\'] = 1
data.loc[data[\'m_work_14\']<0,\'m_work_14\'] = 2
#和同龄人相比社会经济地位
data.loc[data[\'status_peer\']<0,\'status_peer\'] = 2
#和3年前比社会经济地位
data.loc[data[\'status_3_before\']<0,\'status_3_before\'] = 2
#对‘观点’处理
data.loc[data[\'view\']<0,\'view\'] = 4
#对期望年收入处理
data.loc[data[\'inc_ability\']<=0,\'inc_ability\']= 2
inc_exp_mean = data[\'inc_exp\'].mean()
data.loc[data[\'inc_exp\']<=0,\'inc_exp\']= inc_exp_mean #取均值
#部分特征处理,取众数(首先去除缺失值的数据)
for i in range(1,9+1):
data.loc[data[\'public_service_\'+str(i)]<0,\'public_service_\'+str(i)] = int(data[\'public_service_\'+str(i)].dropna().mode().values)
for i in range(1,13+1):
data.loc[data[\'trust_\'+str(i)]<0,\'trust_\'+str(i)] = int(data[\'trust_\'+str(i)].dropna().mode().values)
#上面的循环要加上int,因为values返回一个array是1*1的,那么跟右边的长度匹配不上
# 转换成int就可以广播赋值
数据增广
上述只是对原始的特征进行处理,下面我们需要进一步分析特征的关系,引入更多有可能具有较大重要性的特征来协助判断。
#第一次结婚年龄 147
data[\'marital_1stbir\'] = data[\'marital_1st\'] - data[\'birth\']
#最近结婚年龄 148
data[\'marital_nowtbir\'] = data[\'marital_now\'] - data[\'birth\']
#是否再婚 149
data[\'mar\'] = data[\'marital_nowtbir\'] - data[\'marital_1stbir\']
#配偶年龄 150
data[\'marital_sbir\'] = data[\'marital_now\']-data[\'s_birth\']
#配偶年龄差 151
data[\'age_\'] = data[\'marital_nowtbir\'] - data[\'marital_sbir\']
#收入比 151+7 =158
data[\'income/s_income\'] = data[\'income\']/(data[\'s_income\']+1) #同居伴侣
data[\'income+s_income\'] = data[\'income\']+(data[\'s_income\']+1)
data[\'income/family_income\'] = data[\'income\']/(data[\'family_income\']+1)
data[\'all_income/family_income\'] = (data[\'income\']+data[\'s_income\'])/(data[\'family_income\']+1)
data[\'income/inc_exp\'] = data[\'income\']/(data[\'inc_exp\']+1)
data[\'family_income/m\'] = data[\'family_income\']/(data[\'family_m\']+0.01)
data[\'income/m\'] = data[\'income\']/(data[\'family_m\']+0.01)
#收入/面积比 158+4=162
data[\'income/floor_area\'] = data[\'income\']/(data[\'floor_area\']+0.01)
data[\'all_income/floor_area\'] = (data[\'income\']+data[\'s_income\'])/(data[\'floor_area\']+0.01)
data[\'family_income/floor_area\'] = data[\'family_income\']/(data[\'floor_area\']+0.01)
data[\'floor_area/m\'] = data[\'floor_area\']/(data[\'family_m\']+0.01)
#class 162+3=165
data[\'class_10_diff\'] = (data[\'class_10_after\'] - data[\'class\'])
data[\'class_diff\'] = data[\'class\'] - data[\'class_10_before\']
data[\'class_14_diff\'] = data[\'class\'] - data[\'class_14\']
#悠闲指数 166
leisure_fea_lis = [\'leisure_\'+str(i) for i in range(1,13)]
data[\'leisure_sum\'] = data[leisure_fea_lis].sum(axis=1) #skew
#满意指数 167
public_service_fea_lis = [\'public_service_\'+str(i) for i in range(1,10)]
data[\'public_service_sum\'] = data[public_service_fea_lis].sum(axis=1) #skew
#信任指数 168
trust_fea_lis = [\'trust_\'+str(i) for i in range(1,14)]
data[\'trust_sum\'] = data[trust_fea_lis].sum(axis=1) #skew
#province mean 168+13=181
data[\'province_income_mean\'] = data.groupby([\'province\'])[\'income\'].transform(\'mean\').values
data[\'province_family_income_mean\'] = data.groupby([\'province\'])[\'family_income\'].transform(\'mean\').values
data[\'province_equity_mean\'] = data.groupby([\'province\'])[\'equity\'].transform(\'mean\').values
data[\'province_depression_mean\'] = data.groupby([\'province\'])[\'depression\'].transform(\'mean\').values
data[\'province_floor_area_mean\'] = data.groupby([\'province\'])[\'floor_area\'].transform(\'mean\').values
data[\'province_health_mean\'] = data.groupby([\'province\'])[\'health\'].transform(\'mean\').values
data[\'province_class_10_diff_mean\'] = data.groupby([\'province\'])[\'class_10_diff\'].transform(\'mean\').values
data[\'province_class_mean\'] = data.groupby([\'province\'])[\'class\'].transform(\'mean\').values
data[\'province_health_problem_mean\'] = data.groupby([\'province\'])[\'health_problem\'].transform(\'mean\').values
data[\'province_family_status_mean\'] = data.groupby([\'province\'])[\'family_status\'].transform(\'mean\').values
data[\'province_leisure_sum_mean\'] = data.groupby([\'province\'])[\'leisure_sum\'].transform(\'mean\').values
data[\'province_public_service_sum_mean\'] = data.groupby([\'province\'])[\'public_service_sum\'].transform(\'mean\').values
data[\'province_trust_sum_mean\'] = data.groupby([\'province\'])[\'trust_sum\'].transform(\'mean\').values
#city mean 181+13=194
data[\'city_income_mean\'] = data.groupby([\'city\'])[\'income\'].transform(\'mean\').values #按照city分组
data[\'city_family_income_mean\'] = data.groupby([\'city\'])[\'family_income\'].transform(\'mean\').values
data[\'city_equity_mean\'] = data.groupby([\'city\'])[\'equity\'].transform(\'mean\').values
data[\'city_depression_mean\'] = data.groupby([\'city\'])[\'depression\'].transform(\'mean\').values
data[\'city_floor_area_mean\'] = data.groupby([\'city\'])[\'floor_area\'].transform(\'mean\').values
data[\'city_health_mean\'] = data.groupby([\'city\'])[\'health\'].transform(\'mean\').values
data[\'city_class_10_diff_mean\'] = data.groupby([\'city\'])[\'class_10_diff\'].transform(\'mean\').values
data[\'city_class_mean\'] = data.groupby([\'city\'])[\'class\'].transform(\'mean\').values
data[\'city_health_problem_mean\'] = data.groupby([\'city\'])[\'health_problem\'].transform(\'mean\').values
data[\'city_family_status_mean\'] = data.groupby([\'city\'])[\'family_status\'].transform(\'mean\').values
data[\'city_leisure_sum_mean\'] = data.groupby([\'city\'])[\'leisure_sum\'].transform(\'mean\').values
data[\'city_public_service_sum_mean\'] = data.groupby([\'city\'])[\'public_service_sum\'].transform(\'mean\').values
data[\'city_trust_sum_mean\'] = data.groupby([\'city\'])[\'trust_sum\'].transform(\'mean\').values
#county mean 194 + 13 = 207
data[\'county_income_mean\'] = data.groupby([\'county\'])[\'income\'].transform(\'mean\').values
data[\'county_family_income_mean\'] = data.groupby([\'county\'])[\'family_income\'].transform(\'mean\').values
data[\'county_equity_mean\'] = data.groupby([\'county\'])[\'equity\'].transform(\'mean\').values
data[\'county_depression_mean\'] = data.groupby([\'county\'])[\'depression\'].transform(\'mean\').values
data[\'county_floor_area_mean\'] = data.groupby([\'county\'])[\'floor_area\'].transform(\'mean\').values
data[\'county_health_mean\'] = data.groupby([\'county\'])[\'health\'].transform(\'mean\').values
data[\'county_class_10_diff_mean\'] = data.groupby([\'county\'])[\'class_10_diff\'].transform(\'mean\').values
data[\'county_class_mean\'] = data.groupby([\'county\'])[\'class\'].transform(\'mean\').values
data[\'county_health_problem_mean\'] = data.groupby([\'county\'])[\'health_problem\'].transform(\'mean\').values
data[\'county_family_status_mean\'] = data.groupby([\'county\'])[\'family_status\'].transform(\'mean\').values
data[\'county_leisure_sum_mean\'] = data.groupby([\'county\'])[\'leisure_sum\'].transform(\'mean\').values
data[\'county_public_service_sum_mean\'] = data.groupby([\'county\'])[\'public_service_sum\'].transform(\'mean\').values
data[\'county_trust_sum_mean\'] = data.groupby([\'county\'])[\'trust_sum\'].transform(\'mean\').values
#ratio 相比同省 207 + 13 =220
data[\'income/province\'] = data[\'income\']/(data[\'province_income_mean\'])
data[\'family_income/province\'] = data[\'family_income\']/(data[\'province_family_income_mean\'])
data[\'equity/province\'] = data[\'equity\']/(data[\'province_equity_mean\'])
data[\'depression/province\'] = data[\'depression\']/(data[\'province_depression_mean\'])
data[\'floor_area/province\'] = data[\'floor_area\']/(data[\'province_floor_area_mean\'])
data[\'health/province\'] = data[\'health\']/(data[\'province_health_mean\'])
data[\'class_10_diff/province\'] = data[\'class_10_diff\']/(data[\'province_class_10_diff_mean\'])
data[\'class/province\'] = data[\'class\']/(data[\'province_class_mean\'])
data[\'health_problem/province\'] = data[\'health_problem\']/(data[\'province_health_problem_mean\'])
data[\'family_status/province\'] = data[\'family_status\']/(data[\'province_family_status_mean\'])
data[\'leisure_sum/province\'] = data[\'leisure_sum\']/(data[\'province_leisure_sum_mean\'])
data[\'public_service_sum/province\'] = data[\'public_service_sum\']/(data[\'province_public_service_sum_mean\'])
data[\'trust_sum/province\'] = data[\'trust_sum\']/(data[\'province_trust_sum_mean\']+1)
#ratio 相比同市 220 + 13 =233
data[\'income/city\'] = data[\'income\']/(data[\'city_income_mean\'])
data[\'family_income/city\'] = data[\'family_income\']/(data[\'city_family_income_mean\'])
data[\'equity/city\'] = data[\'equity\']/(data[\'city_equity_mean\'])
data[\'depression/city\'] = data[\'depression\']/(data[\'city_depression_mean\'])
data[\'floor_area/city\'] = data[\'floor_area\']/(data[\'city_floor_area_mean\'])
data[\'health/city\'] = data[\'health\']/(data[\'city_health_mean\'])
data[\'class_10_diff/city\'] = data[\'class_10_diff\']/(data[\'city_class_10_diff_mean\'])
data[\'class/city\'] = data[\'class\']/(data[\'city_class_mean\'])
data[\'health_problem/city\'] = data[\'health_problem\']/(data[\'city_health_problem_mean\'])
data[\'family_status/city\'] = data[\'family_status\']/(data[\'city_family_status_mean\'])
data[\'leisure_sum/city\'] = data[\'leisure_sum\']/(data[\'city_leisure_sum_mean\'])
data[\'public_service_sum/city\'] = data[\'public_service_sum\']/(data[\'city_public_service_sum_mean\'])
data[\'trust_sum/city\'] = data[\'trust_sum\']/(data[\'city_trust_sum_mean\'])
#ratio 相比同个地区 233 + 13 =246
data[\'income/county\'] = data[\'income\']/(data[\'county_income_mean\'])
data[\'family_income/county\'] = data[\'family_income\']/(data[\'county_family_income_mean\'])
data[\'equity/county\'] = data[\'equity\']/(data[\'county_equity_mean\'])
data[\'depression/county\'] = data[\'depression\']/(data[\'county_depression_mean\'])
data[\'floor_area/county\'] = data[\'floor_area\']/(data[\'county_floor_area_mean\'])
data[\'health/county\'] = data[\'health\']/(data[\'county_health_mean\'])
data[\'class_10_diff/county\'] = data[\'class_10_diff\']/(data[\'county_class_10_diff_mean\'])
data[\'class/county\'] = data[\'class\']/(data[\'county_class_mean\'])
data[\'health_problem/county\'] = data[\'health_problem\']/(data[\'county_health_problem_mean\'])
data[\'family_status/county\'] = data[\'family_status\']/(data[\'county_family_status_mean\'])
data[\'leisure_sum/county\'] = data[\'leisure_sum\']/(data[\'county_leisure_sum_mean\'])
data[\'public_service_sum/county\'] = data[\'public_service_sum\']/(data[\'county_public_service_sum_mean\'])
data[\'trust_sum/county\'] = data[\'trust_sum\']/(data[\'county_trust_sum_mean\'])
#age mean 246+ 13 =259
data[\'age_income_mean\'] = data.groupby([\'age\'])[\'income\'].transform(\'mean\').values
data[\'age_family_income_mean\'] = data.groupby([\'age\'])[\'family_income\'].transform(\'mean\').values
data[\'age_equity_mean\'] = data.groupby([\'age\'])[\'equity\'].transform(\'mean\').values
data[\'age_depression_mean\'] = data.groupby([\'age\'])[\'depression\'].transform(\'mean\').values
data[\'age_floor_area_mean\'] = data.groupby([\'age\'])[\'floor_area\'].transform(\'mean\').values
data[\'age_health_mean\'] = data.groupby([\'age\'])[\'health\'].transform(\'mean\').values
data[\'age_class_10_diff_mean\'] = data.groupby([\'age\'])[\'class_10_diff\'].transform(\'mean\').values
data[\'age_class_mean\'] = data.groupby([\'age\'])[\'class\'].transform(\'mean\').values
data[\'age_health_problem_mean\'] = data.groupby([\'age\'])[\'health_problem\'].transform(\'mean\').values
data[\'age_family_status_mean\'] = data.groupby([\'age\'])[\'family_status\'].transform(\'mean\').values
data[\'age_leisure_sum_mean\'] = data.groupby([\'age\'])[\'leisure_sum\'].transform(\'mean\').values
data[\'age_public_service_sum_mean\'] = data.groupby([\'age\'])[\'public_service_sum\'].transform(\'mean\').values
data[\'age_trust_sum_mean\'] = data.groupby([\'age\'])[\'trust_sum\'].transform(\'mean\').values
# 和同龄人相比259 + 13 =272
data[\'income/age\'] = data[\'income\']/(data[\'age_income_mean\'])
data[\'family_income/age\'] = data[\'family_income\']/(data[\'age_family_income_mean\'])
data[\'equity/age\'] = data[\'equity\']/(data[\'age_equity_mean\'])
data[\'depression/age\'] = data[\'depression\']/(data[\'age_depression_mean\'])
data[\'floor_area/age\'] = data[\'floor_area\']/(data[\'age_floor_area_mean\'])
data[\'health/age\'] = data[\'health\']/(data[\'age_health_mean\'])
data[\'class_10_diff/age\'] = data[\'class_10_diff\']/(data[\'age_class_10_diff_mean\'])
data[\'class/age\'] = data[\'class\']/(data[\'age_class_mean\'])
data[\'health_problem/age\'] = data[\'health_problem\']/(data[\'age_health_problem_mean\'])
data[\'family_status/age\'] = data[\'family_status\']/(data[\'age_family_status_mean\'])
data[\'leisure_sum/age\'] = data[\'leisure_sum\']/(data[\'age_leisure_sum_mean\'])
data[\'public_service_sum/age\'] = data[\'public_service_sum\']/(data[\'age_public_service_sum_mean\'])
data[\'trust_sum/age\'] = data[\'trust_sum\']/(data[\'age_trust_sum_mean\'])
经过上述的处理,特征扩充为272维,而经过分析发现应该删除掉有效样本数过少的特征:
#删除数值特别少的和之前用过的特征
del_list=[\'id\',\'survey_time\',\'edu_other\',\'invest_other\',\'property_other\',\'join_party\',\'province\',\'city\',\'county\']
use_feature = [clo for clo in data.columns if clo not in del_list]
data.fillna(0,inplace=True) #还是补0
train_shape = train.shape[0] #一共的数据量,训练集
features = data[use_feature].columns #删除后所有的特征
X_train_263 = data[:train_shape][use_feature].values
y_train = target
X_test_263 = data[train_shape:][use_feature].values
X_train_263.shape #最终一种263个特征
再结合个人经验,挑选出最重要的49个特征:
imp_fea_49 = [\'equity\',\'depression\',\'health\',\'class\',\'family_status\',\'health_problem\',\'class_10_after\',
\'equity/province\',\'equity/city\',\'equity/county\',
\'depression/province\',\'depression/city\',\'depression/county\',
\'health/province\',\'health/city\',\'health/county\',
\'class/province\',\'class/city\',\'class/county\',
\'family_status/province\',\'family_status/city\',\'family_status/county\',
\'family_income/province\',\'family_income/city\',\'family_income/county\',
\'floor_area/province\',\'floor_area/city\',\'floor_area/county\',
\'leisure_sum/province\',\'leisure_sum/city\',\'leisure_sum/county\',
\'public_service_sum/province\',\'public_service_sum/city\',\'public_service_sum/county\',
\'trust_sum/province\',\'trust_sum/city\',\'trust_sum/county\',
\'income/m\',\'public_service_sum\',\'class_diff\',\'status_3_before\',\'age_income_mean\',\'age_floor_area_mean\',
\'weight_jin\',\'height_cm\',
\'health/age\',\'depression/age\',\'equity/age\',\'leisure_sum/age\'
]
train_shape = train.shape[0]
X_train_49 = data[:train_shape][imp_fea_49].values
X_test_49 = data[train_shape:][imp_fea_49].values
# X_train_49.shape #最重要的49个特征
再将其中一些特征转换为one-hot特征:
from sklearn import preprocessing
cat_fea = [\'survey_type\',\'gender\',\'nationality\',\'edu_status\',\'political\',\'hukou\',\'hukou_loc\',\'work_exper\',\'work_status\',\'work_type\',
\'work_manage\',\'marital\',\'s_political\',\'s_hukou\',\'s_work_exper\',\'s_work_status\',\'s_work_type\',\'f_political\',\'f_work_14\',
\'m_political\',\'m_work_14\'] #已经是0、1的值不需要onehot
noc_fea = [clo for clo in use_feature if clo not in cat_fea]
onehot_data = data[cat_fea].values
enc = preprocessing.OneHotEncoder(categories = \'auto\')
oh_data=enc.fit_transform(onehot_data).toarray()
oh_data.shape #变为onehot编码格式
X_train_oh = oh_data[:train_shape,:]
X_test_oh = oh_data[train_shape:,:]
X_train_oh.shape #其中的训练集
X_train_383 = np.column_stack([data[:train_shape][noc_fea].values,X_train_oh])#先是noc,再是cat_fea
X_test_383 = np.column_stack([data[train_shape:][noc_fea].values,X_test_oh])
# X_train_383.shape
最终得到为383个特征。
模型构建
此处模型构建的主要流程为:
- 构建多个集成分类算法进行训练,并对验证集进行预测
- 将各个基础集成分类算法对验证集的预测作为训练数据,验证集的标签作为训练标签,由此来训练一个回归模型对各个基础集成分类算法进行融合,得到较好的结果
具体处理的流程是创建一个模型,然后对其采用五折交叉验证的方式去训练,并且对验证集和测试集进行预测,多个模型得到的验证集预测进行堆叠得到下一层的训练数据,而多个模型得到的测试集预测直接进行平均求和,以此给训练好的下一层做出真正对测试集的预测。
对原始263维特征进行处理
LightGBM
lgb_263_param = { # 这是训练的参数列表
\"num_leaves\":7,
\"min_data_in_leaf\": 20, # 一个叶子上最小分配到的数量,用来处理过拟合
\"objective\": \"regression\", # 设置类型为回归
\"max_depth\": -1, # 限制树的最大深度,-1代表没有限制
\"learning_rate\": 0.003,
\"boosting\": \"gbdt\", # 用gbdt算法
\"feature_fraction\": 0.18, # 每次迭代时使用18%的特征参与建树,引入特征子空间的多样性
\"bagging_freq\": 1, # 每一次迭代都执行bagging
\"bagging_fraction\": 0.55, # 每次bagging在不进行重采样的情况下随机选择55%数据训练
\"bagging_seed\": 14,
\"metric\": \'mse\',
\"lambda_l1\": 0.1,
\"lambda_l2\": 0.2,
\"verbosity\": -1 # 打印消息的详细程度
}
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state = 4)
# 产生一个容器,可以用来对对数据集进行打乱的5次切分,以此来进行五折交叉验证
oof_lgb_263 = np.zeros(len(X_train_263))
predictions_lgb_263 = np.zeros(len(X_test_263))
for fold_, (train_idx, valid_idx) in enumerate(folds.split(X_train_263, y_train)):
# 切分后返回的训练集和验证集的索引
print(\"fold n{}\".format(fold_+1)) # 当前第几折
train_data_now = lgb.Dataset(X_train_263[train_idx], y_train[train_idx])
valid_data_now = lgb.Dataset(X_train_263[valid_idx], y_train[valid_idx])
# 取出数据并转换为lgb的数据
num_round = 10000
lgb_263 = lgb.train(lgb_263_param, train_data_now, num_round,
valid_sets=[train_data_now, valid_data_now], verbose_eval=500,
early_stopping_rounds = 800)
# 第一个参数是原始参数,第二个是用来训练的数据,第三个参数代表迭代次数
# 第四个参数是训练后评估所用的数据,第五个参数是每多少次迭代就打印下当前的评估信息
# 第六个参数是超过多少次迭代没有变化就停止
oof_lgb_263[valid_idx] = lgb_263.predict(X_train_263[valid_idx],
num_iteration=lgb_263.best_iteration)
predictions_lgb_263 += lgb_263.predict(X_test_263, num_iteration=
lgb_263.best_iteration) / folds.n_splits
# 这是将预测概率进行平均
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_lgb_263, target)))
# 它是回归类型因此不能用正确率来衡量
由于这次打印出来的信息过多,因此我只补充最终的分数:
CV score: 0.45153757
而我们可以利用lightGBM中的特征重要性来直观展现各个特征的重要性程度:
pd.set_option(\"display.max_columns\", None) # 设置可以显示的最大行和最大列
pd.set_option(\'display.max_rows\', None) # 如果超过就显示省略号,none表示不省略
#设置value的显示长度为100,默认为50
pd.set_option(\'max_colwidth\',100)
# 创建,然后只有一列就是刚才所使用的的特征
df = pd.DataFrame(data[use_feature].columns.tolist(), columns=[\'feature\'])
df[\'importance\'] = list(lgb_263.feature_importance())
df = df.sort_values(by=\'importance\', ascending=False) # 降序排列
plt.figure(figsize = (14,28))
sns.barplot(x=\'importance\', y=\'feature\', data = df.head(50))# 取出前五十个画图
plt.title(\'Features importance (averaged/folds)\')
plt.tight_layout() # 自动调整适应范围
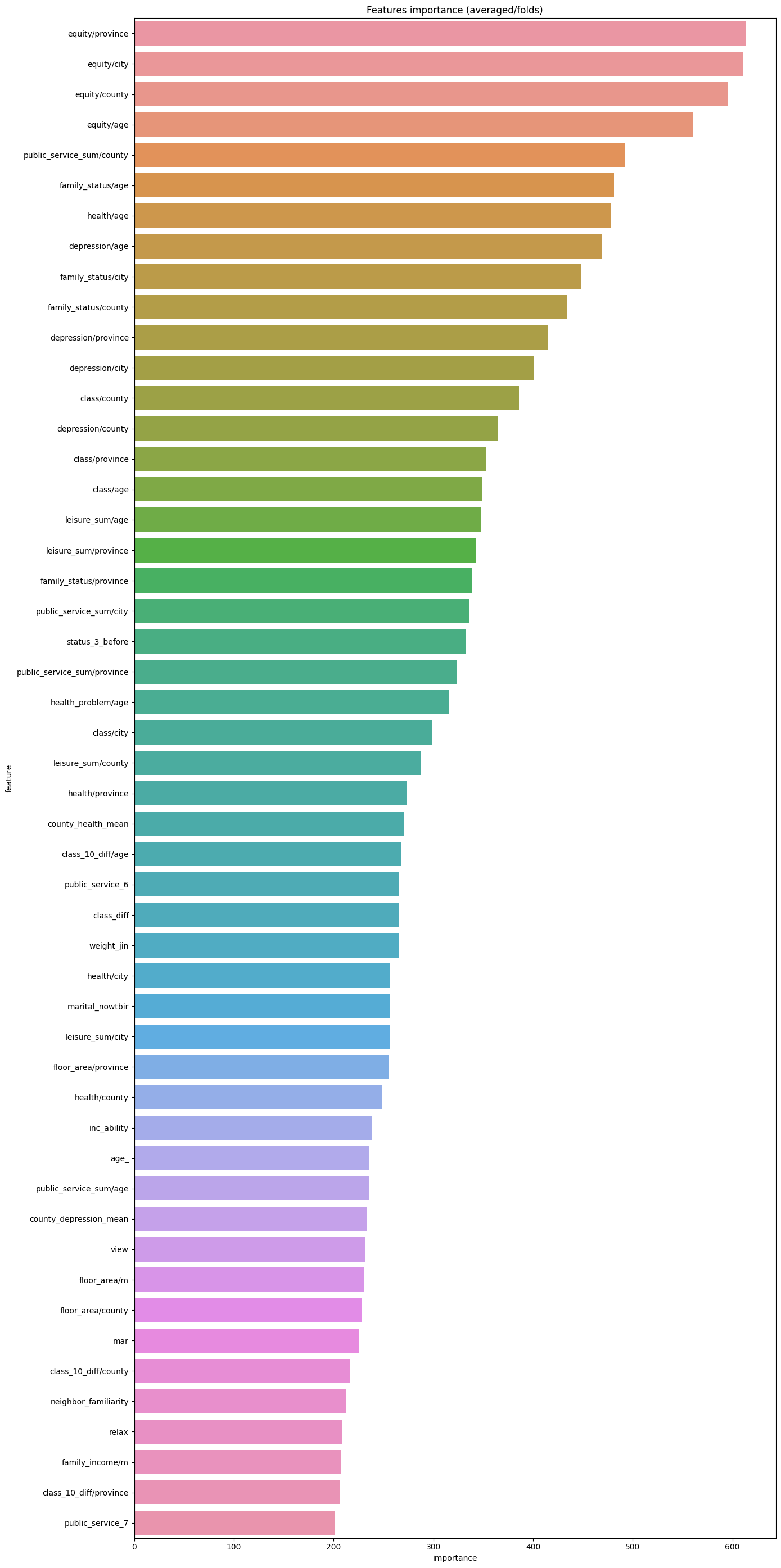
可以看到最重要的特征为同龄人的健康程度,这方面还是很符合直观感觉的。
xgBoost
xgb_263_params = {
\"eta\":0.02, # 学习率
\"max_depth\": 6, # 树的最大深度
\"min_child_weight\":3, # 划分为叶结点所含样本的最小权重和
\"gamma\":0, # 在分裂时损失最小应该减少gamma,越大则越减少过拟合
\"subsample\":0.7, # 控制对于每棵树随机采样的比例
\"colsample_bytree\":0.3, # 用来控制每棵树对于特征的采样占比
\"lambda\":2,
\"objective\":\"reg:linear\",
\"eval_metric\":\"rmse\",
\"verbosity\":1, # 打印消息的详细程度
\"nthread\":-1 # 并行线程数,使用最大
}
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=2019)
oof_xgb_263 = np.zeros(len(X_train_263))
predictions_xgb_263 = np.zeros(len(X_test_263))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
print(\"fold n°{}\".format(fold_+1))
trn_data = xgb.DMatrix(X_train_263[trn_idx], y_train[trn_idx])
val_data = xgb.DMatrix(X_train_263[val_idx], y_train[val_idx])
watchlist = [(trn_data, \'train\'), (val_data, \'valid_data\')]
xgb_263 = xgb.train(dtrain=trn_data, num_boost_round=3000, evals=watchlist,
early_stopping_rounds=600, verbose_eval=500,
params=xgb_263_params)
oof_xgb_263[val_idx] = xgb_263.predict(xgb.DMatrix(X_train_263[val_idx]),
ntree_limit=xgb_263.best_ntree_limit)
predictions_xgb_263 += xgb_263.predict(xgb.DMatrix(X_test_263), ntree_limit=
xgb_263.best_ntree_limit) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_xgb_263, target)))
CV score: 0.45402538
随机森林
#RandomForestRegressor随机森林
folds = KFold(n_splits=5, shuffle=True, random_state=2019)
oof_rfr_263 = np.zeros(len(X_train_263))
predictions_rfr_263 = np.zeros(len(X_test_263))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_263[trn_idx]
tr_y = y_train[trn_idx]
rfr_263 = rfr(n_estimators=1600,max_depth=9, min_samples_leaf=9,
min_weight_fraction_leaf=0.0,max_features=0.25,
verbose=1,n_jobs=-1) #并行化
#verbose = 0 为不在标准输出流输出日志信息
#verbose = 1 为输出进度条记录
#verbose = 2 为每个epoch输出一行记录
rfr_263.fit(tr_x,tr_y)
oof_rfr_263[val_idx] = rfr_263.predict(X_train_263[val_idx])
predictions_rfr_263 += rfr_263.predict(X_test_263) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_rfr_263, target)))
CV score: 0.47810816
梯度提升GBDT
#GradientBoostingRegressor梯度提升决策树
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=2018)
oof_gbr_263 = np.zeros(train_shape)
predictions_gbr_263 = np.zeros(len(X_test_263))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_263[trn_idx]
tr_y = y_train[trn_idx]
gbr_263 = gbr(n_estimators=400, learning_rate=0.01,subsample=0.65,max_depth=7, min_samples_leaf=20,
max_features=0.22,verbose=1)
gbr_263.fit(tr_x,tr_y)
oof_gbr_263[val_idx] = gbr_263.predict(X_train_263[val_idx])
predictions_gbr_263 += gbr_263.predict(X_test_263) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_gbr_263, target)))
CV score: 0.45781356
极端随机森林回归
#ExtraTreesRegressor 极端随机森林回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_etr_263 = np.zeros(train_shape)
predictions_etr_263 = np.zeros(len(X_test_263))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_263[trn_idx]
tr_y = y_train[trn_idx]
etr_263 = etr(n_estimators=1000,max_depth=8, min_samples_leaf=12, min_weight_fraction_leaf=0.0,
max_features=0.4,verbose=1,n_jobs=-1)# max_feature:划分时考虑的最大特征数
etr_263.fit(tr_x,tr_y)
oof_etr_263[val_idx] = etr_263.predict(X_train_263[val_idx])
predictions_etr_263 += etr_263.predict(X_test_263) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_etr_263, target)))
CV score: 0.48598827
综上,我们得到了五个模型的预测结果、模型架构以及参数。那么我们需要对这五个模型进行融合,可以用一个Kernel Ridge Regression,核脊回归来进行融合,这个回归有点类似于岭回归,也是采用五折交叉验证重复两次:
train_stack2 = np.vstack([oof_lgb_263,oof_xgb_263,oof_gbr_263,oof_rfr_263,oof_etr_263]).transpose()
# transpose()函数的作用就是调换x,y,z的位置,也就是数组的索引值,变成zyx
# 本来是5*验证集样本数*1,变成1*验证集样本数*5,二维矩阵每一行是单个样本在5个模型上的预测结果,行数是样本数
test_stack2 = np.vstack([predictions_lgb_263, predictions_xgb_263,predictions_gbr_263,predictions_rfr_263,predictions_etr_263]).transpose()
# 变成1*测试集样本数*5,二维矩阵每一行是单个测试集样本在5个模型上的预测结果,行数是样本数
#交叉验证:5折,重复2次
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack2 = np.zeros(train_stack2.shape[0])
predictions_lr2 = np.zeros(test_stack2.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack2,target)):
print(\"fold {}\".format(fold_))
trn_data, trn_y = train_stack2[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack2[val_idx], target.iloc[val_idx].values
#Kernel Ridge Regression
lr2 = kr()
lr2.fit(trn_data, trn_y)
oof_stack2[val_idx] = lr2.predict(val_data)
predictions_lr2 += lr2.predict(test_stack2) / 10
mean_squared_error(target.values, oof_stack2)
0.44815130114230267
对49维的特征进行处理
同样我们可以对49维度的特征进行类似处理,我将代码总结如下:
##### lgb_49
lgb_49_param = {
\'num_leaves\': 9,
\'min_data_in_leaf\': 23,
\'objective\':\'regression\',
\'max_depth\': -1,
\'learning_rate\': 0.002,
\"boosting\": \"gbdt\",
\"feature_fraction\": 0.45,
\"bagging_freq\": 1,
\"bagging_fraction\": 0.65,
\"bagging_seed\": 15,
\"metric\": \'mse\',
\"lambda_l2\": 0.2,
\"verbosity\": -1} # 一个叶子上数据的最小数量 \\ feature_fraction将会在每棵树训练之前选择 45% 的特征。可以用来加速训练,可以用来处理过拟合。 #bagging_fraction不进行重采样的情况下随机选择部分数据。可以用来加速训练,可以用来处理过拟合。
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=9)
oof_lgb_49 = np.zeros(len(X_train_49))
predictions_lgb_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print(\"fold n°{}\".format(fold_+1))
trn_data = lgb.Dataset(X_train_49[trn_idx], y_train[trn_idx])
val_data = lgb.Dataset(X_train_49[val_idx], y_train[val_idx])
num_round = 12000
lgb_49 = lgb.train(lgb_49_param, trn_data, num_round, valid_sets = [trn_data, val_data], verbose_eval=1000, early_stopping_rounds = 1000)
oof_lgb_49[val_idx] = lgb_49.predict(X_train_49[val_idx], num_iteration=lgb_49.best_iteration)
predictions_lgb_49 += lgb_49.predict(X_test_49, num_iteration=lgb_49.best_iteration) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_lgb_49, target)))
##### xgb_49
xgb_49_params = {\'eta\': 0.02,
\'max_depth\': 5,
\'min_child_weight\':3,
\'gamma\':0,
\'subsample\': 0.7,
\'colsample_bytree\': 0.35,
\'lambda\':2,
\'objective\': \'reg:linear\',
\'eval_metric\': \'rmse\',
\'silent\': True,
\'nthread\': -1}
folds = KFold(n_splits=5, shuffle=True, random_state=2019)
oof_xgb_49 = np.zeros(len(X_train_49))
predictions_xgb_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print(\"fold n°{}\".format(fold_+1))
trn_data = xgb.DMatrix(X_train_49[trn_idx], y_train[trn_idx])
val_data = xgb.DMatrix(X_train_49[val_idx], y_train[val_idx])
watchlist = [(trn_data, \'train\'), (val_data, \'valid_data\')]
xgb_49 = xgb.train(dtrain=trn_data, num_boost_round=3000, evals=watchlist, early_stopping_rounds=600, verbose_eval=500, params=xgb_49_params)
oof_xgb_49[val_idx] = xgb_49.predict(xgb.DMatrix(X_train_49[val_idx]), ntree_limit=xgb_49.best_ntree_limit)
predictions_xgb_49 += xgb_49.predict(xgb.DMatrix(X_test_49), ntree_limit=xgb_49.best_ntree_limit) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_xgb_49, target)))
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=2018)
oof_gbr_49 = np.zeros(train_shape)
predictions_gbr_49 = np.zeros(len(X_test_49))
#GradientBoostingRegressor梯度提升决策树
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
gbr_49 = gbr(n_estimators=600, learning_rate=0.01,subsample=0.65,max_depth=6, min_samples_leaf=20,
max_features=0.35,verbose=1)
gbr_49.fit(tr_x,tr_y)
oof_gbr_49[val_idx] = gbr_49.predict(X_train_49[val_idx])
predictions_gbr_49 += gbr_49.predict(X_test_49) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_gbr_49, target)))
这里由于特征数目较少,只考虑使用3个基础模型,接下来便是进行融合:
train_stack3 = np.vstack([oof_lgb_49,oof_xgb_49,oof_gbr_49]).transpose()
test_stack3 = np.vstack([predictions_lgb_49, predictions_xgb_49,predictions_gbr_49]).transpose()
#
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack3 = np.zeros(train_stack3.shape[0])
predictions_lr3 = np.zeros(test_stack3.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack3,target)):
print(\"fold {}\".format(fold_))
trn_data, trn_y = train_stack3[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack3[val_idx], target.iloc[val_idx].values
#Kernel Ridge Regression
lr3 = kr()
lr3.fit(trn_data, trn_y)
oof_stack3[val_idx] = lr3.predict(val_data)
predictions_lr3 += lr3.predict(test_stack3) / 10
mean_squared_error(target.values, oof_stack3)
0.4662728551415085
对383维的特征进行处理
这里对383维度的特征采用刚才类似的方法是可以的,但是也可以采用其他的方法,例如我们将基模型换成普通的回归模型:
Kernel Ridge Regression 基于核的岭回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_kr_383 = np.zeros(train_shape)
predictions_kr_383 = np.zeros(len(X_test_383))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_383, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_383[trn_idx]
tr_y = y_train[trn_idx]
#Kernel Ridge Regression 岭回归
kr_383 = kr()
kr_383.fit(tr_x,tr_y)
oof_kr_383[val_idx] = kr_383.predict(X_train_383[val_idx])
predictions_kr_383 += kr_383.predict(X_test_383) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_kr_383, target)))
CV score: 0.51412085
可以看到普通回归的误差相比于集成算法会高一些。
普通岭回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_ridge_383 = np.zeros(train_shape)
predictions_ridge_383 = np.zeros(len(X_test_383))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_383, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_383[trn_idx]
tr_y = y_train[trn_idx]
#使用岭回归
ridge_383 = Ridge(alpha=1200)
ridge_383.fit(tr_x,tr_y)
oof_ridge_383[val_idx] = ridge_383.predict(X_train_383[val_idx])
predictions_ridge_383 += ridge_383.predict(X_test_383) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_ridge_383, target)))
CV score: 0.48687670
ElasticNet 弹性网络
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_en_383 = np.zeros(train_shape)
predictions_en_383 = np.zeros(len(X_test_383))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_383, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_383[trn_idx]
tr_y = y_train[trn_idx]
#ElasticNet 弹性网络
en_383 = en(alpha=1.0,l1_ratio=0.06)
en_383.fit(tr_x,tr_y)
oof_en_383[val_idx] = en_383.predict(X_train_383[val_idx])
predictions_en_383 += en_383.predict(X_test_383) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_en_383, target)))
CV score: 0.53296555
BayesianRidge 贝叶斯岭回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_br_383 = np.zeros(train_shape)
predictions_br_383 = np.zeros(len(X_test_383))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_383, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_383[trn_idx]
tr_y = y_train[trn_idx]
#BayesianRidge 贝叶斯回归
br_383 = br()
br_383.fit(tr_x,tr_y)
oof_br_383[val_idx] = br_383.predict(X_train_383[val_idx])
predictions_br_383 += br_383.predict(X_test_383) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_br_383, target)))
CV score: 0.48717310
那么对383特征的四次回归也进行融合:
train_stack1 = np.vstack([oof_br_383,oof_kr_383,oof_en_383,oof_ridge_383]).transpose()
test_stack1 = np.vstack([predictions_br_383, predictions_kr_383,predictions_en_383,predictions_ridge_383]).transpose()
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack1 = np.zeros(train_stack1.shape[0])
predictions_lr1 = np.zeros(test_stack1.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack1,target)):
print(\"fold {}\".format(fold_))
trn_data, trn_y = train_stack1[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack1[val_idx], target.iloc[val_idx].values
# LinearRegression简单的线性回归
lr1 = lr()
lr1.fit(trn_data, trn_y)
oof_stack1[val_idx] = lr1.predict(val_data)
predictions_lr1 += lr1.predict(test_stack1) / 10
mean_squared_error(target.values, oof_stack1)
0.4878202780283125
对49维特征的继续处理
由于49维的特征是最重要的特征,所以这里考虑增加更多的模型进行49维特征的数据的构建工作。加入跟383特征一样的回归模型,具体如下:
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_kr_49 = np.zeros(train_shape)
predictions_kr_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
kr_49 = kr()
kr_49.fit(tr_x,tr_y)
oof_kr_49[val_idx] = kr_49.predict(X_train_49[val_idx])
predictions_kr_49 += kr_49.predict(X_test_49) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_kr_49, target)))
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_ridge_49 = np.zeros(train_shape)
predictions_ridge_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
ridge_49 = Ridge(alpha=6)
ridge_49.fit(tr_x,tr_y)
oof_ridge_49[val_idx] = ridge_49.predict(X_train_49[val_idx])
predictions_ridge_49 += ridge_49.predict(X_test_49) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_ridge_49, target)))
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_br_49 = np.zeros(train_shape)
predictions_br_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
br_49 = br()
br_49.fit(tr_x,tr_y)
oof_br_49[val_idx] = br_49.predict(X_train_49[val_idx])
predictions_br_49 += br_49.predict(X_test_49) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_br_49, target)))
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_en_49 = np.zeros(train_shape)
predictions_en_49 = np.zeros(len(X_test_49))
#
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print(\"fold n°{}\".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
en_49 = en(alpha=1.0,l1_ratio=0.05)
en_49.fit(tr_x,tr_y)
oof_en_49[val_idx] = en_49.predict(X_train_49[val_idx])
predictions_en_49 += en_49.predict(X_test_49) / folds.n_splits
print(\"CV score: {:<8.8f}\".format(mean_squared_error(oof_en_49, target)))
再进行融合:
train_stack4 = np.vstack([oof_br_49,oof_kr_49,oof_en_49,oof_ridge_49]).transpose()
test_stack4 = np.vstack([predictions_br_49, predictions_kr_49,predictions_en_49,predictions_ridge_49]).transpose()
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack4 = np.zeros(train_stack4.shape[0])
predictions_lr4 = np.zeros(test_stack4.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack4,target)):
print(\"fold {}\".format(fold_))
trn_data, trn_y = train_stack4[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack4[val_idx], target.iloc[val_idx].values
#LinearRegression
lr4 = lr()
lr4.fit(trn_data, trn_y)
oof_stack4[val_idx] = lr4.predict(val_data)
predictions_lr4 += lr4.predict(test_stack1) / 10
mean_squared_error(target.values, oof_stack4)
0.49491439094008133
模型融合
我们对263、383、49特征的数据总共构建了4个模型,当前就需要对这些模型的预测结果进行融合,也可以通过学习一个回归来进行融合:
train_stack5 = np.vstack([oof_stack1,oof_stack2,oof_stack3,oof_stack4]).transpose()
test_stack5 = np.vstack([predictions_lr1, predictions_lr2,predictions_lr3,predictions_lr4]).transpose()
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack5 = np.zeros(train_stack5.shape[0])
predictions_lr5= np.zeros(test_stack5.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack5,target)):
print(\"fold {}\".format(fold_))
trn_data, trn_y = train_stack5[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack5[val_idx], target.iloc[val_idx].values
#LinearRegression
lr5 = lr()
lr5.fit(trn_data, trn_y)
oof_stack5[val_idx] = lr5.predict(val_data)
predictions_lr5 += lr5.predict(test_stack5) / 10
mean_squared_error(target.values, oof_stack5)
0.4480223491250565
可以看到结果改进了不少。
结果保存
submit_example = pd.read_csv(\'submit_example.csv\',sep=\',\',encoding=\'latin-1\')
submit_example[\'happiness\'] = predictions_lr5
submit_example.loc[submit_example[\'happiness\']>4.96,\'happiness\']= 5
submit_example.loc[submit_example[\'happiness\']<=1.04,\'happiness\']= 1
submit_example.loc[(submit_example[\'happiness\']>1.96)&(submit_example[\'happiness\']<2.04),\'happiness\']= 2
# 进行整数解的近似
submit_example.to_csv(\"submision.csv\",index=False)
集成学习案例2——蒸汽量预测
背景介绍
锅炉的燃烧效率的影响因素很多,包括锅炉的可调参数,如燃烧给量,一二次风,引风,返料风,给水水量;以及锅炉的工况,比如锅炉床温、床压,炉膛温度、压力,过热器的温度等。我们如何使用以上的信息,根据锅炉的工况,预测产生的蒸汽量呢?
数据分成训练数据(train.txt)和测试数据(test.txt),其中字段”V0”-“V37”,这38个字段是作为特征变量,”target”作为目标变量。我们需要利用训练数据训练出模型,预测测试数据的目标变量。
最终的评价指标为均方误差MSE
具体代码
导入需要的包
import warnings
warnings.filterwarnings(\"ignore\") # 忽略各种不影响正常运行的警告
import matplotlib.pyplot as plt
import seaborn as sns
# 模型
import pandas as pd
import numpy as np
from scipy import stats
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV, RepeatedKFold, cross_val_score,cross_val_predict,KFold
from sklearn.metrics import make_scorer,mean_squared_error
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
from sklearn.svm import LinearSVR, SVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor,AdaBoostRegressor
from xgboost import XGBRegressor
from sklearn.preprocessing import PolynomialFeatures,MinMaxScaler,StandardScaler
加载数据
data_train = pd.read_csv(\"train.txt\", sep=\'\\t\')
data_test = pd.read_csv(\"test.txt\", sep = \'\\t\')
# 对训练和测试的数据集叠在一起,对特征处理的时候比较方便
data_train[\'oringin\'] = \'train\'
data_test[\'oringin\'] = \'test\'
data_all = pd.concat([data_train, data_test], axis = 0, ignore_index = True)
# 按照上下的方式叠在一起,并且忽略掉原来的索引,叠后重新建立索引
data_all.head()
data_all.tail() # target列自动填充NaN

探索数据分布
这里因为是传感器的数据,即连续变量,所以使用 kdeplot(核密度估计图) 进行数据的初步分析,即EDA:
for column in data_all.columns[0:-2]:
# 为每个特征画一个核密度估计图
g = sns.kdeplot(data_all[column][(data_all[\'oringin\'] == \"train\")], color=\'Red\',
shade=True) # 在曲线下面绘制阴影
g = sns.kdeplot(data_all[column][(data_all[\"oringin\"] == \"test\")], color=\'Blue\',
ax=g, shade=True) # ax=g还是在原来的画柄上
g.set_xlabel(column)
g.set_ylabel(\"Frequency\")
g = g.legend([\"train\", \"test\"])
plt.show()
这里为每个特征都画出了一个核密度的图,太多了我就放一个吧。
那么我们观察所有的图片,可以发现某些特征的训练数据和测试数据的分布存在很大的差异,例如下图:
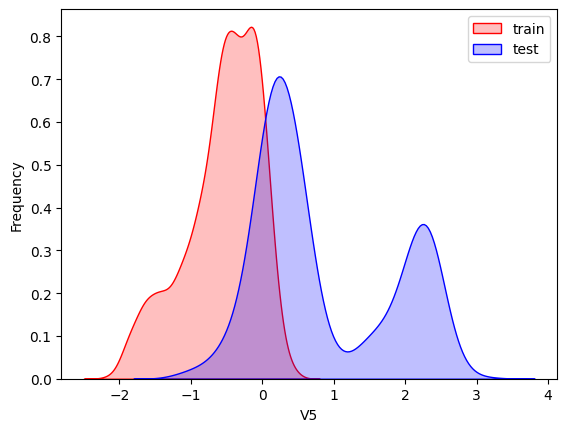
那我们的选择是删除这些数据:
# 从以上的图中可以看出特征\"V5\",\"V9\",\"V11\",\"V17\",\"V22\",\"V28\"中
# 训练集数据分布和测试集数据分布不均,所以我们删除这些特征数据
for column in [\"V5\",\"V9\",\"V11\",\"V17\",\"V22\",\"V28\"]:
g = sns.kdeplot(data_all[column][(data_all[\"oringin\"] == \"train\")], color=\"Red\", shade = True)
g = sns.kdeplot(data_all[column][(data_all[\"oringin\"] == \"test\")], ax =g, color=\"Blue\", shade= True)
g.set_xlabel(column)
g.set_ylabel(\"Frequency\")
g = g.legend([\"train\",\"test\"])
plt.show()
data_all.drop([\"V5\",\"V9\",\"V11\",\"V17\",\"V22\",\"V28\"],axis=1,inplace=True)
# inplace 代表在原来的数据上做删除操作
剩下的特征,我们可以查看彼此之间的相关性:
# 查看特征之之间的相关性
data_train1 = data_all[data_all[\"oringin\"] == \"train\"].drop(\"oringin\", axis=1)
plt.figure(figsize=(25,20))
colnm = data_train1.columns.tolist() # 得到特征名称构成的列表
mcorr = data_train1[colnm].corr(method=\"spearman\") # 计算特征之间的相关系数矩阵
mask = np.zeros_like(mcorr, dtype=np.bool) # 构造与mcorr同维度的矩阵,bool类型
mask[np.triu_indices_from(mask)] = True # 里面那个是返回方阵的上三角的索引
cmap = sns.diverging_palette(220, 10, as_cmap = True)
# 从220和10之间建立一个逐渐变化色板对象
g = sns.heatmap(mcorr, mask = mask, cmap = cmap, square = True,
annot = True, fmt=\'0.2f\')
# 第一个为数据集,cmap为颜色条的名称或者对象或者列表,annot代表是否写入数值,
# square将每个单元格设置为方形
plt.show()
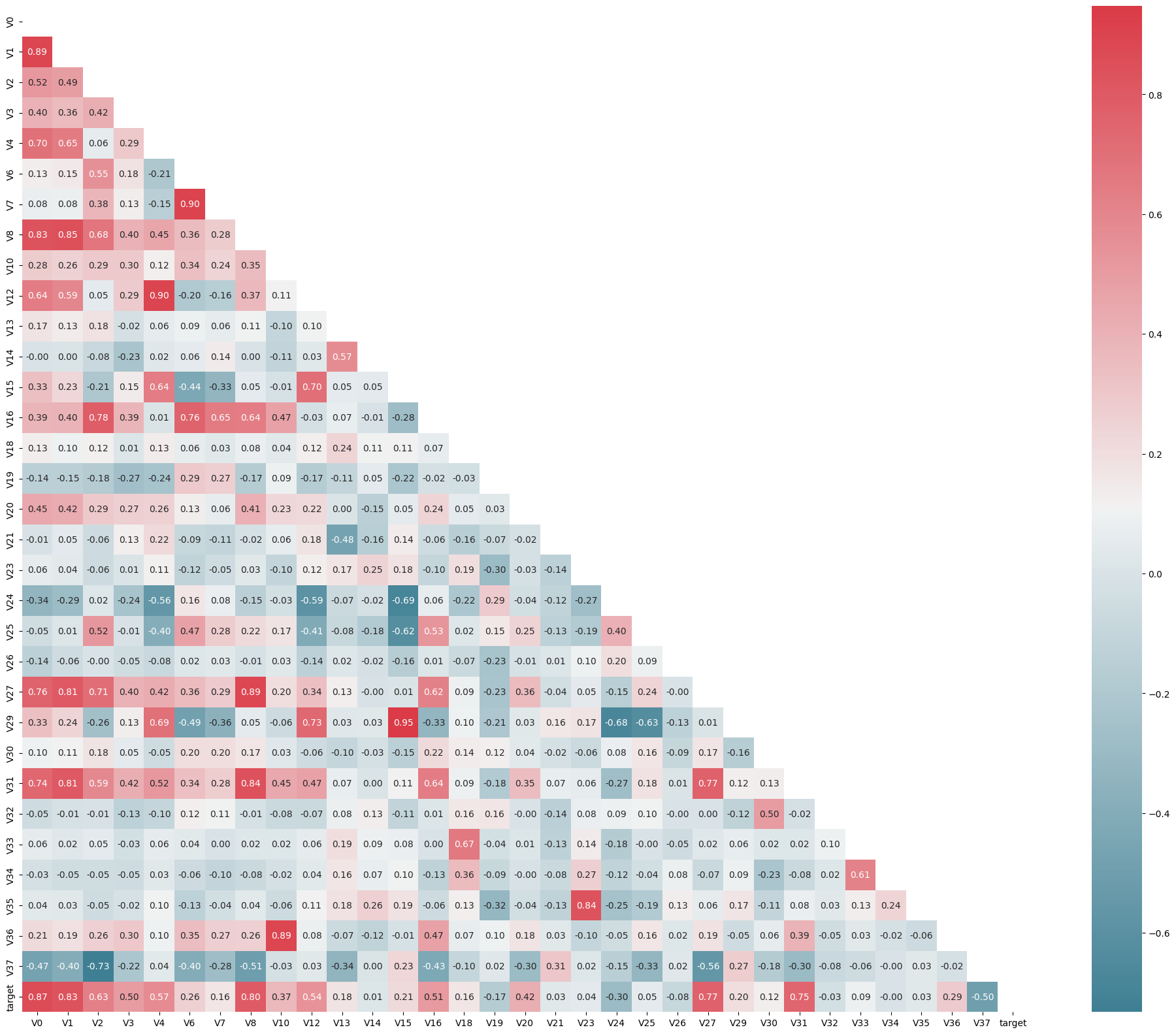
可以看到部分特征之间的相关性较强。而部分特征与标签列的相关性太小,可以认为这些特征的贡献很有限,因此可以进行删除:
# 将与target相关性过小的特征进行删除
threshold = 0.1
corr_matrix = data_train1.corr().abs() # 相关系数矩阵的绝对值
drop_col = corr_matrix[corr_matrix[\"target\"] < threshold ].index
print(drop_col)
data_all.drop(drop_col, axis=1, inplace=True)
Index([\'V14\', \'V21\', \'V25\', \'V26\', \'V32\', \'V33\', \'V34\'], dtype=\'object\')
接下来需要对数据进行归一化操作:
# 进行归一化操作
cols_numeric = list(data_all.columns) # 当前的特征列表
cols_numeric.remove(\"oringin\") # 拿掉这一列
def scale_minmax(col):
return (col-col.min()) / (col.max() - col.min())
scale_cols = [col for col in cols_numeric if col != \"target\"] # 除了目标,相当于remove
data_all[scale_cols] = data_all[scale_cols].apply(scale_minmax, axis = 0)
data_all[scale_cols].describe()
特征工程
这里引入了一个Box-Cox变换,因为大部分假设对数据有一定的要求,那我们希望数据的特征能够尽量满足正态分布的关系,而ox-cox变换的目标有两个:一个是变换后,可以一定程度上减小不可观测的误差和预测变量的相关性。主要操作是对因变量转换,使得变换后的因变量于回归自变量具有线性相依关系,误差也服从正态分布,误差各分量是等方差且相互独立。第二个是用这个变换来使得因变量获得一些性质,比如在时间序列分析中的平稳性,或者使得因变量分布为正态分布。
下面我们可以先观察变换前和变换后的区别:
fcols = 6
frows = len(cols_numeric) - 1 # 因为target不用
plt.figure(figsize = (4*fcols, 4*frows))
i = 0
for var in cols_numeric:
if var != \"target\":
data_tem = data_all[[var, \"target\"]].dropna() # 取出当前列和taget列并舍弃缺失值
# 画处理前分布图
i+=1
plt.subplot(frows, fcols, i)
sns.distplot(data_tem[var], fit = stats.norm)
# 画出直方图,并且用stats.norm来进行拟合
plt.title(var+\"oringinal\")
plt.xlabel(\"\")
# 画QQ图,看数据分布是否服从正态分布
i+=1
plt.subplot(frows, fcols, i)
_ = stats.probplot(data_tem[var],plot = plt)
plt.title(\"skew=\" + \"{:.4f}\".format(stats.skew(data_tem[var])))
# stats.skew是计算偏度
plt.xlabel(\"\")
plt.ylabel(\"\")
# 画散点图
i+=1
plt.subplot(frows, fcols, i)
plt.plot(data_tem[var], data_tem[\"target\"], \".\", alpha = 0.5)
# 横轴为var特征,纵轴为target,用.来画,透明度为0.5
plt.title(\"corr=\" + \"{:.2f}\".format(np.corrcoef(data_tem[var],
data_tem[\"target\"])[0][1]))
# 画boxcox变换后的直方图
i+=1
plt.subplot(frows, fcols, i)
trans_var, lambda_var = stats.boxcox(data_tem[var].dropna() + 1)
trans_var = scale_minmax(trans_var)
sns.distplot(trans_var, fit = stats.norm)
plt.title(var+\"Transformed\")
plt.xlabel(\"\")
# 画处理后的QQ图
i+=1
plt.subplot(frows,fcols,i)
_=stats.probplot(trans_var, plot=plt)
plt.title(\'skew=\'+\'{:.4f}\'.format(stats.skew(trans_var)))
plt.xlabel(\'\')
plt.ylabel(\'\')
# 画处理后的散点图
i+=1
plt.subplot(frows,fcols,i)
plt.plot(trans_var, data_tem[\'target\'],\'.\',alpha=0.5)
plt.title(\'corr=\'+\'{:.2f}\'.format(np.corrcoef(trans_var,
data_tem[\'target\'])[0][1]))
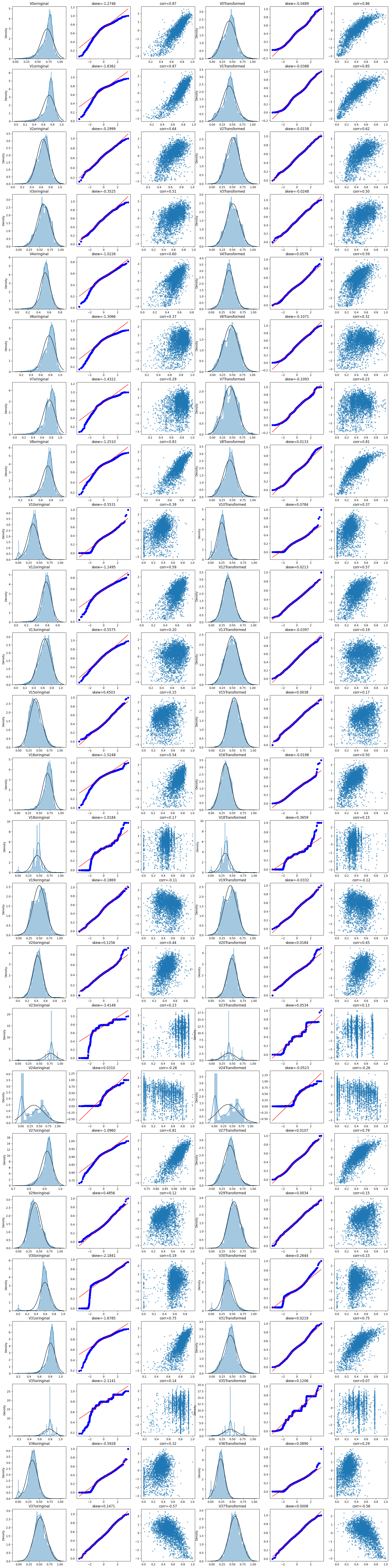
从QQ图中可以看到经过变换后,其正态性好了很多!
因此对总体进行变换:
# 进行boxcox变换
cols_transform = data_all.columns[0:-2] # 这些是需要变换的特征
for col in cols_transform:
data_all.loc[:, col], _ = stats.boxcox(data_all.loc[:,col] + 1)
# 因为我们已经标准化到-1与+1之间,而该函数要求输入数据是正的,因此+1
print(data_all.target.describe())
count 2888.000000
mean 0.126353
std 0.983966
min -3.044000
25% -0.350250
50% 0.313000
75% 0.793250
max 2.538000
Name: target, dtype: float64
而对于标签列来说也是如此,我们同样可以对其尝试进行变换,使用对数变换target目标值提升特征数据的正太性:
# 变化之前
plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
sns.distplot(data_all.target.dropna(), fit = stats.norm)
plt.subplot(1,2,2)
_ = stats.probplot(data_all.target.dropna(), plot = plt)
# 掉target使用对数变化来提升其正态性质
sp = data_train.target
data_train.target1 = np.power(1.5, sp)
plt.figure(figsize=(12,4))
plt.subplot(1,2,1)
sns.distplot(data_train.target1.dropna(),fit=stats.norm);
plt.subplot(1,2,2)
_=stats.probplot(data_train.target1.dropna(), plot=plt)
模型构建与集成学习
构建数据集
# 构建训练集与测试集
from sklearn.model_selection import train_test_split
def get_training_data():
df_train = data_all[data_all[\"oringin\"] == \"train\"]
df_train[\"label\"] = data_train.target1 # 这是经过对数变化的标签
y = df_train.target
X = df_train.drop([\"oringin\",\"target\",\"label\"],axis =1)
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size = 0.3,
random_state = 100)
return X_train, X_valid, y_train, y_valid
def get_test_data():
df_test = data_all[data_all[\"oringin\"] == \"test\"].reset_index(drop=True)
# 因为获取的测试集的标签是后面的,那么需要从零开始,因此重置
return df_test.drop([\"oringin\", \"target\"], axis = 1)
构建评估函数
# 自己实现评估函数
from sklearn.metrics import make_scorer
def rmse(y_true, y_pred):
diff = y_pred - y_true
sum_sq = sum(diff * 2)
n = len(y_pred)
return np.sqrt(sum_sq / n)
def mse(y_true, y_pred):
return mean_squared_error(y_true, y_pred)
rmse_scorer = make_scorer(rmse, greater_is_better = False)
# 构建损失函数对象,第二个参数为True代表值越大越好,False代表值越小越好
mse_scorer = make_scorer(mse, greater_is_better = False)
构建寻找离群值的函数
# 该函数用来寻找离群值
def find_outliers(model, X, y, sigma = 3):
model.fit(X, y)
y_pred = pd.Series(model.predict(X), index = y.index)
resid = y - y_pred
mean_resid = resid.mean()
std_resid = resid.std()
z = (resid - mean_resid) / std_resid # 将差距标准化
outliers = z[abs(z) > sigma].index # 那些离平均差距超过sigma的
print(\"R2 = \", model.score(X, y))
print(\"rmse = \",rmse(y, y_pred))
print(\"mse = \", mean_squared_error(y, y_pred))
print(\"--\" * 20)
print(\"mean of residuals:\", mean_resid)
print(\"std of residuals:\", std_resid)
print(\"--\" * 20)
print(len(outliers), \"outliers:\")
print(outliers.tolist())
plt.figure(figsize = (15,5))
ax_131 = plt.subplot(1,3,1)
plt.plot(y, y_pred,\'.\')
plt.plot(y.loc[outliers], y_pred.loc[outliers], \"ro\")
plt.legend([\"Accepted\",\"Outlier\"])
plt.xlabel(\"y\")
plt.ylabel(\"y_pred\")
ax_132 = plt.subplot(1,3,2)
plt.plot(y, y- y_pred, \".\")
plt.plot(y.loc[outliers], y.loc[outliers] - y_pred.loc[outliers], \"ro\")
plt.legend([\'Accepted\',\'Outlier\'])
plt.xlabel(\'y\')
plt.ylabel(\'y - y_pred\');
ax_133 = plt.subplot(1,3,3)
z.plot.hist(bins =50, ax = ax_133) # 画出z的直方图
z.loc[outliers].plot.hist(color=\'r\', bins = 50, ax = ax_133)
plt.legend([\'Accepted\',\'Outlier\'])
plt.xlabel(\'z\')
return outliers
尝试用岭回归去寻找离散值:
X_train, X_valid, y_train, y_valid = get_training_data()
test = get_test_data()
outliers = find_outliers(Ridge(), X_train, y_train)
# 先用简单的岭回归去拟合试试看
X_outliers=X_train.loc[outliers]
y_outliers=y_train.loc[outliers]
X_t=X_train.drop(outliers)
y_t=y_train.drop(outliers)
R2 = 0.8766692297367809
rmse = nan
mse = 0.12180705697820839
----------------------------------------
mean of residuals: 1.8875439448847292e-16
std of residuals: 0.3490950551088699
----------------------------------------
22 outliers:
[2655, 2159, 1164, 2863, 1145, 2697, 2528, 2645, 691, 1085, 1874, 2647, 884, 2696, 2668, 1310, 1901, 1458, 2769, 2002, 2669, 1972]
可以看到效果很好。
模型训练
def get_trainning_data_omitoutliers():
#获取训练数据省略异常值
y=y_t.copy()
X=X_t.copy()
return X,y
def train_model(model, param_grid = [], X = [], y = [], splits = 5, repeats = 5):
# 尝试实现训练函数
if(len(y) == 0):
X, y = get_trainning_data_omitoutliers()
# 交叉验证
rkfold = RepeatedKFold(n_splits = splits, n_repeats = repeats)
# 网格搜索参数
if(len(param_grid) > 0):
gsearch = GridSearchCV(model, param_grid, cv = rkfold,
scoring = \"neg_mean_squared_error\",
verbose = 1, return_train_score = True)
gsearch.fit(X, y)
model = gsearch.best_estimator_
best_idx = gsearch.best_index_ # 最佳参数在param_gird中的索引
# 获取交叉验证评价指标
grid_results = pd.DataFrame(gsearch.cv_results_)
cv_mean = abs(grid_results.loc[best_idx, \"mean_test_score\"])
cv_std = grid_results.loc[best_idx, \"std_test_score\"]
else: # 不进行网格搜索
grid_results = []
cv_results = cross_val_score(model, X ,y, scoring = \"neg_mean_squared_error\",
cv =rkfold)
cv_mean = abs(np.mean(cv_results))
cv_std = np.std(cv_results)
# 合并数据
cv_score = pd.Series({\"mean\":cv_mean, \"std\":cv_std})
# 预测
y_pred = model.predict(X)
# 模型性能的统计数据
print(\'----------------------\')
print(model)
print(\'----------------------\')
print(\'score=\',model.score(X,y))
print(\'rmse=\',rmse(y, y_pred))
print(\'mse=\',mse(y, y_pred))
print(\'cross_val: mean=\',cv_mean,\', std=\',cv_std)
# 残差分析与可视化
y_pred = pd.Series(y_pred,index=y.index)
resid = y - y_pred
mean_resid = resid.mean()
std_resid = resid.std()
z = (resid - mean_resid)/std_resid
n_outliers = sum(abs(z)>3)
outliers = z[abs(z)>3].index
return model, cv_score, grid_results
用岭回归来进行拟合:
# 定义训练变量存储数据
opt_models = dict()
score_models = pd.DataFrame(columns=[\'mean\',\'std\'])
splits=5
repeats=5
model = \'RandomForest\' #可替换,见案例分析一的各种模型
opt_models[model] = Ridge() #可替换,见案例分析一的各种模型
alph_range = np.arange(0.25,6,0.25)
param_grid = {\'alpha\': alph_range}
opt_models[model],cv_score,grid_results = train_model(opt_models[model],
param_grid=param_grid,
splits=splits, repeats=repeats)
cv_score.name = model
score_models = score_models.append(cv_score)
plt.figure()
plt.errorbar(alph_range, abs(grid_results[\'mean_test_score\']),
abs(grid_results[\'std_test_score\'])/np.sqrt(splits*repeats))
plt.xlabel(\'alpha\')
plt.ylabel(\'score\')
Ridge(alpha=0.25)
----------------------
score= 0.8926884445023296
rmse= 5.109572960503552e-08
mse= 0.10540676395670681
cross_val: mean= 0.10910070303768438 , std= 0.005867873719733897
修改模型
我认为岭回归比较简单,因此尝试将模型改为随机森林回归,但是一直跑不动,因此自己写了比较简单的训练过程。
先大概给个范围进行随机网格搜索:
from sklearn.model_selection import RandomizedSearchCV
n_estimators_range=[int(x) for x in np.linspace(start=50,stop=500,num=50)]
max_depth_range=[5,10,15]
max_depth_range.append(None)
min_samples_split_range=[2,5,10]
min_samples_leaf_range=[4,8]
random_forest_seed = 1
random_forest_hp_range={\'n_estimators\':n_estimators_range,
\'max_depth\':max_depth_range,
\'min_samples_split\':min_samples_split_range,
\'min_samples_leaf\':min_samples_leaf_range
}
X, y = get_trainning_data_omitoutliers()
random_forest_model_test_base=RandomForestRegressor()
random_forest_model_test_random=RandomizedSearchCV(estimator=random_forest_model_test_base,
param_distributions=random_forest_hp_range,
n_iter=200,
n_jobs=-1,
cv=5,
verbose=1,
random_state=random_forest_seed
)
random_forest_model_test_random.fit(X,y)
best_hp_now=random_forest_model_test_random.best_params_
print(best_hp_now)
{\'n_estimators\': 343, \'min_samples_split\': 2, \'min_samples_leaf\': 4, \'max_depth\': None}
再根据这个参数,缩小范围进行网格搜索:
n_estimators_range=[int(x) for x in np.linspace(start=320,stop=370,num=10)]
max_depth_range=[5,10,15]
max_depth_range.append(None)
min_samples_split_range=[1,2,3,4,5]
min_samples_leaf_range=[2,3,4,5,6]
random_forest_seed = 1
random_forest_hp_range_2={\'n_estimators\':n_estimators_range,
\'max_depth\':max_depth_range,
\'min_samples_split\':min_samples_split_range,
\'min_samples_leaf\':min_samples_leaf_range
}
random_forest_model_test_2_base=RandomForestRegressor()
random_forest_model_test_2_random = GridSearchCV(estimator=random_forest_model_test_2_base,
param_grid=random_forest_hp_range_2,
cv=5,
verbose=1,
n_jobs=-1)
random_forest_model_test_2_random.fit(X,y)
best_hp_now_2=random_forest_model_test_2_random.best_params_
print(best_hp_now_2)
{\'max_depth\': None, \'min_samples_leaf\': 2, \'min_samples_split\': 3, \'n_estimators\': 364}
因此接下来做出预测并保存:
random_forest_model_final=random_forest_model_test_2_random.best_estimator_
y_predict = pd.DataFrame(random_forest_model_final.predict(test))
y_predict.to_csv(\"predict.txt\", header = None,index = False)
完结!
来源:https://www.cnblogs.com/FavoriteStar/p/16925544.html
本站部分图文来源于网络,如有侵权请联系删除。
 百木园
百木园